基礎知識
簡分數:分子和分母均為整數的分數。
繁分數:如果分數形式中,分子或分母含有四則運算或分數,或分子與分母都含有四則運算或分數的數。
約分:把一個分數化成同它相等,但分子、分母都比較小的分數,叫做約分。
約分的方法:用分子和分母的公因數(1除外)去除分數的分子和分母。通常要除到得出最簡分數為止。
最簡分數:分子和分母為互質數的分數。最簡分數的分數的分子與分母沒有除1以外的其他公約數。最簡分數又叫既約分數,既約分數可理解成已經約分過的分數,也就是分子和分母是互質數的分數。
簡分數與最簡分數
簡分數,是分子和分母均為整數的分數。
最簡分數,是分子、分母只有公因數1的分數,或者說分子和分母互質的分數,又稱既約分數。
兩者的關係為:最簡分數一定是簡分數,簡分數不一定是最簡分數。
 簡分數
簡分數 簡分數
簡分數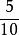 簡分數
簡分數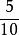 簡分數
簡分數例如:是最簡分數,一定是簡分數。是簡分數,但不是最簡分數。
簡分數與繁分數
繁分數是指分子或分母含有四則運算或分數,或分子與分母都含有四則運算或分數的數。繁分數是數,不是除法式子。一個有意義的除法算式應包括定義範圍內的被除數、除數和除號,它是一種運算表達形式。只有通過運算後,才能得出一個商數來,所以除法算式和數是兩回事。
根據繁分數的特點和內涵,考慮到既有分數的“形”,又要有分子或分母含有四則運算或分數,或分子與分母都含有四則運算或分數的特殊情況。
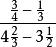 簡分數
簡分數 簡分數
簡分數例如,是繁分數,不是簡分數。是簡分數。
相關計算
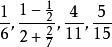 簡分數
簡分數例1.判斷下列數字是否為簡分數:。
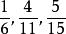 簡分數
簡分數解:由分子和分母均為整數的分數為簡分數的定義可知,均為簡分數。
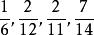 簡分數
簡分數例2.判斷下列簡分數是否為最簡分數,不是的話,將其化簡為最簡分數:。
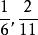 簡分數
簡分數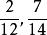 簡分數
簡分數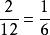 簡分數
簡分數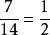 簡分數
簡分數解:分子和分母為互質數的分數為最簡分數。由其定義可知為最簡分數。為簡分數,並不是最簡分數。其化簡為,。
教學套用
在簡分數的學習中,到做到掌握簡分數的具體定義,以及簡分數與繁分數的區別和簡分數向最簡分數的化簡內容。在簡分數的教學中,應該淡化其概念的規範性、嚴謹性,強化學生對簡分數的個性化理解與體驗。可以從創設問題情境開始,讓學生歷經感受、猜想、例證、感悟等過程。在這個過程中,學生可以憑藉自己對簡分數的初步理解和表層感受,對簡分數進行了大膽的猜想,從而使得學生明顯個性色彩的想法和思維得以暴露。想法的正確與否是次要的,重要的是學生有機會表達自己對新知識的最真實的感受與理解,這些想法為學生進一步抽象出簡分數的本質提供了寶貴的資源。再藉助這些片面、幼稚甚至錯誤的想法展開思考與論證,在思想交鋒中,簡分數的本質屬性如抽絲剝繭般由模糊變得清晰起來。這一做法不僅有效地調動了學生學習的積極性,轉變學生的學習方式,而且充分注重了知識結論的動態生成過程。

