名稱簡介
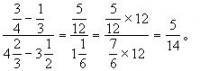繁分數繁分數的定義
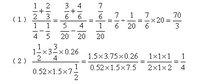繁分數
繁分數一、繁分數是分數形式的數，但不是分數
數叫做分數。定義中的“形”是指分子、分母和分數線 構成了分數的“形”。m和n都是整數，且n≠0是指分子、分母的取值範圍，兩者有機地結合，構成了分數的整體，全面地揭示了分數的內涵，同時也確定了分數的全部外延。
和主分數線，這三部分構成了繁分數的“形”。這和分數的“形”是類似的。我們可以說繁分數是分數形式的數。但是，繁分數的分子部分分母部分含有分數，或分子部分分母部分都含有分數，這和分數的分子分母比，取值範圍擴大了，和分數的定義相悖，所以繁分數不是分數，也不是什麼特殊的分數。
二、繁分數是數，而不是除法式子
一個有意義的除法算式應包括定義範圍內的被除數、除數和除號，它是一種運算表達形式。只有通過運算後，才能得出一個商數來，所以除法算式和一個數是兩回事。
個類似分數的數來表示，即用
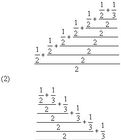繁分數三、繁分數定義的表述
根據繁分數的特點和內涵，考慮到既有分數的“形”，又有分子部分分母部分含有分數的特殊情況，它的定義可以這樣表述：如分數形式，分子或分母含有分數，或分子與分母都含有分數的數，叫繁分數。
在一個繁分數里，最長的分數線叫做繁分數的主分數線，主分數線上下不管有多少個數或運算，都把它們分別看作是繁分數的分子和分母。
