算法教學
正文
亦稱算法式教學。控制學生解題過程的一種教學方法其代表人物為蘇聯心理學家Л.Н.蘭達。早在20世紀50年代初期,蘭達從思維的構造觀點出發,研究構造心理學的執行原則,探討了思考活動的結構—操作問題。他認為,使學生掌握了思考活動的一般方法,就可以形成和發展學生的智力。因此,他著手探索學生解題的合理思考模式問題。開始,他企圖通過經驗分析法來確定合理思考模式,結果發現所定的思考模式,缺乏可靠的客觀檢驗標準。後來,受到控制論、資訊理論與數理邏輯的啟示,改用模擬—實驗法來探討合理思考的模式。在此基礎上,他於20世紀60年代初,提出了用來控制解題過程的兩種思考模式,即算法式模式與非算法式模式(1962年曾稱為機率模式,1975年稱為啟發式模式)。1961年,蘭達在其《學生的合理思維方法和算法教學問題》一文中,介紹了他在算法教學方面的初步實驗成果。
蘭達所說的算法,泛指單義的解題活動方法的指令系統,也就是用以解決問題的一整套規定了的操作程式。例如,為了解決求三角形面積這一問題,可以有這樣一些算法:①用底乘以高,然後把所得的積乘以 1/2(或除以2);②用高乘以底,然後把所得的積乘以1/2(或除以 2);③用底乘以1/2(或除以2),以其結果乘以高等等。這些都是以描述的形式來表示求三角形面積的活動方法的指令。在這些指令中,完備地和單義地規定了求三角形面積的活動應進行的一些操作。按這些操作程式去做,就能導致問題的解決;這種指令系統或操作程式就其功能方面來說,就是所謂算法。
算法可以有不同的表現形式,除上述那種描述形式外,有時常以流程圖的形式來表示。蘭達在研究辨認句型的算法時,所用的算法就是以流程圖形式來表示的。下圖就是蘭達提供的在辨認俄語中簡單句類型時所用的算法模式。
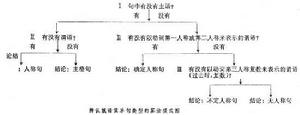 算法教學
算法教學為了有效地實施算法教學,蘭達認為,首先要對能用算法解決的問題,建立其智力活動的算法模式。在建立這種算法模式時,除了要對所解決的問題作邏輯的結構分析以外,還要考慮到心理因素,使確定的算法符合心理過程的形成及其規律。其次,所定算法,從操作量方面來說,也應該是合理的。最後,擬定的算法模式,須通過實驗的檢驗,證明其普遍有效,才能被認為是合理的。
蘭達雖然十分重視算法以及算法教學的作用,但他認為不是所有的問題都能建立或必須套用算法來解決。事實上,有些問題或因其算法難以確定;或雖能確定算法,但實際並不需用這種算法。因此,教學上除了要重視建立算法模式及實施算法式教學以外,還應重視建立啟發式模式及實施啟發式教學。
