簡介
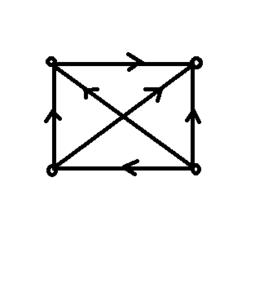
競賽圖是通過在無向完整圖中為每個邊緣分配方向而獲得的有向圖(有向圖)。 也就是說,它是一個完整圖形的方向,等價於一個有向圖,其中每對不同的頂點通過單個有向邊連線,即每對頂點之間都有一條邊相連的有向圖稱為競賽圖。
蘭多(1953)首先調查了競賽圖的許多重要屬性。競賽圖的當前套用包括投票理論和社會選擇理論的研究等。 競賽圖起源於這樣的圖形解釋:循環賽,其中每個玩家恰好一次遇到每個其他玩家。 在競賽圖中,頂點對應於球員。 每對玩家之間的邊緣從勝者到失敗者。 如果每個玩家都對陣同樣數量的其他玩家,那么這個競賽圖就被稱之為常規競賽圖。
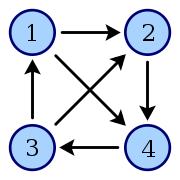 競賽圖
競賽圖路徑和循環
 競賽圖
競賽圖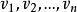 競賽圖
競賽圖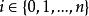 競賽圖
競賽圖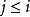 競賽圖
競賽圖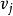 競賽圖
競賽圖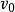 競賽圖
競賽圖任何有限數量n個頂點的競賽圖都包含一個哈密爾頓路徑,即所有n個頂點上的直線路徑。假設該語句適用於n,並考慮n + 1個頂點上的任何競賽圖T。 選擇T的頂點v,並考慮的一個有向路徑。現在讓是最大的,所以對於每個都有一個從到的有向邊。
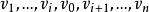 競賽圖
競賽圖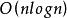 競賽圖
競賽圖是根據需要設定的有向路徑。 這個參數還給出了一種求解哈密爾頓運算元的算法。 只需要檢查邊緣的。
這意味著緊密聯繫的競賽圖有一個哈密爾頓循環(Camion 1959)。 每個聯繫的競賽圖是頂點泛循環:對於每個頂點v,並且每個k在競賽圖中的三個到頂點的數量的範圍內,存在包含v的長度為k的循環。此外,如果比賽是4連線的,則每對頂點可以與哈密爾頓路徑連線(Thomassen 1980)。
傳遞性
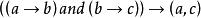 競賽圖
競賽圖在競賽圖中,被叫做一個傳遞。換句話說,在傳遞競賽圖中,頂點(嚴格地)由邊緣關係完全排序。
等價條件
以下語句與n個頂點上的競賽圖T相當:
(1)T具有傳遞性;
(2)T是一個嚴格的總排序;
(3)T是非循環的;
(4)T不包含長度為3的循環;
(5)T的得分序列(外差集)為{0,1,2,...,n-1};
(6)T只有一個哈密爾頓路徑。
拉姆齊理論
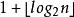 競賽圖
競賽圖傳遞競賽圖在拉姆齊理論中起到類似於無向圖中的作用。 特別是,n個頂點上的每個競賽圖在頂點上包含一個傳遞子公式。證明很簡單:選擇任何一個頂點v作為這個子公式的一部分,並在v的輸入鄰集或v的傳出鄰集之間遞歸地形成其餘的子體,然後取較大者。
縮合
任何比賽的本身就是一場傳遞性的比賽。 因此,即使是不可傳遞的比賽,競賽圖的強力連線組件也可能被完全排序。
得分序列和分數集
比賽的得分序列是比賽頂點的不規則序列。 比賽的得分集是在該比賽中頂點的偏差的整數集合。
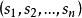 競賽圖
競賽圖Landau的定理(1953):整數序列若且唯若滿足下麵條件的時候是一個得分序列:
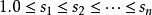 競賽圖
競賽圖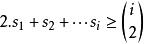 競賽圖
競賽圖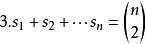 競賽圖
競賽圖讓s(n)是大小為n的不同得分序列的數量。 序列s(n)(OEIS中的序列A000571)開始為:
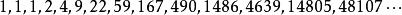 競賽圖
競賽圖溫斯頓和克萊特曼證明,對於足夠大的n:
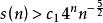 競賽圖
競賽圖其中c= 0.049。
這些提供證據表明:
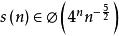 競賽圖
競賽圖這裡φ表示一個漸近緊的界限。
姚明表示,每一個非空的整數都是一些比賽的得分。