立體視覺匹配（Stereo Correspondence）是計算機視覺中的一個重要而又非常困難的問題，它的目標是從不同視點圖像中找到匹配的對應點。
背景
人類的雙目立體視覺系統是一個非常智慧型的系統。場景中的光線在人眼這個精密的成像系統中被採集，通過神經中樞被送入包含有數以億計的神經元的大腦中被並行的處理，得到了實時的高清晰度的準確的深度感覺信息。憑藉著大腦的智慧型與人類的知識，即使是高度近視的人，在摘掉眼鏡之後仍然能夠得到比較準確的深度感。這樣智慧型的系統，使得人類對環境的適應能力大大提高，很多複雜的動作能夠得以完成：如行走、體育運動、駕駛車輛以及進行科學實驗等。
相比之下，機器的立體視覺系統則要落後得多。相機採集到的圖像數據中可能存在較大的噪聲，相機參數也有可能不對稱；用於處理圖像的計算機大部分還是馮~$\cdot$~諾依曼結構的串列計算機，處理能力與人腦相差甚遠。計算機視覺的研究歷史也不長：上世紀七十年代末之前的視覺研究主要集中於生理學和心理學上；在大衛·馬爾提出了視覺計算模型以後，人們才慢慢的開始利用計算機和數學模型進行視覺處理。早期的立體視覺，由於受限於硬體條件，只能對圖像上的特徵點進行匹配，得到離散點的深度信息。然而，計算機硬體的發展非常迅速，正如摩爾定律所指出的，每 18 個月，計算機的硬體價格就下降一半，而性能則提高一倍。當計算機的處理能力不斷提高的時候，人們開始嘗試計算整幅圖的稠密對應關係，同時也開始採用一些更加複雜更加準確的數學工具進行計算。
當前計算機立體視覺的水平與人類的雙目視覺水平還相距甚遠，對它的研究仍然是一個非常活躍的領域。大量的學校、公司以及研究機構的研究人員仍然在進行著對計算機立體視覺的研究，這是因為計算機立體視覺與人眼立體視覺相比，主要有以下不可替代的優點：
* 精度高。人眼的立體感知能力雖然很強，能夠很輕鬆的正確判斷出兩個物體的深度順序，但是卻無法得到其精確的距離信息。然而，使用計算機立體視覺，通過精確的標定，使用合適的計算方法，在匹配正確的情況下可以得到非常精確的深度和位置等數值信息，這使得機器人的精密控制、三維模型重建等工作可以更好的完成。
* 擴展能力強大。由於計算機硬體和軟體不像人類的器官那樣不可改變，計算機立體視覺可以從各個方面對其進行擴展，以滿足不同套用的需求。首先，計算機立體視覺並不限於雙目視覺，很多系統使用了三相機、多相機甚至相機矩陣採集圖像。相機的擺放方式除了類似人眼的水平擺放，還可以採用垂直擺放、環繞擺放以及立體擺放等多種靈活的方式，有一些系統的相機間的關係還可以根據需要進行動態變化。此外，除了可見光，使用特殊的相機，還可以採集到其它各種類型的輸入數據，如紅外線、核磁共振等。所以說，計算機立體視覺技術具有強大的擴展能力，能夠提供比人眼立體視覺系統更豐富的信息。
* 除了以上的兩個特點，計算機還具有連續工作時間長、不易損壞、保密性好、沒有培訓成本、結果易於保存和複製等優點。
由此看來，對於立體視覺匹配的研究，能夠大大的增強計算機或機器人對環境的感知能力，使得機器人能夠更好的適應環境、更加智慧型，從而能夠更好的為人們服務。
如今立體視覺技術主要套用於如下一些領域：三維環境感知與建模、機器人導航、物體跟蹤與檢測以及圖像分割等。隨著立體視覺技術的進一步發展，可能會有更多的領域使用這項技術。
發展與現狀
如前所述，計算機視覺起始於大衛·馬爾等人提出的視覺的可計算模型。最簡單的的匹配算法利用匹配點周圍一個固定大小的視窗的灰度分布，在一個可能的視差範圍內，通過尋找兩個對應視窗圖像向量的歸一化相關值的最大值得到視差，這一類方法也被稱為“區域匹配”方法（AreaMatching）。區域匹配的一個假設是空間的平面是所謂的正平面，也就是與相機平面平行的平面，而實際的場景中存在著大量的非正平面，因此人們開始考慮利用一些更有意義的特徵點（感興趣點）來進行匹配，這種方法也被稱為特徵匹配（Feature Matching）方法，如 Marr和 Poggio 提出了多尺度的匹配算法，利用不同的 Laplacian 過零點以及梯度進行匹配。
立體視覺匹配的另一個挑戰在於匹配的歧義性：對於一幅圖上的某個像素或特徵，另一幅圖像可能有若干特徵與之相似，如何選擇正確的匹配是一個困難而又必須解決的問題。Barn 提出了鬆弛標號法（Relaxation-Labeling），利用平滑性和投票的策略解決歧義性問題；Pollard 等人定義了離散視差的視差梯度，通過限制視差梯度減小歧義情況下的錯匹配；Marr 和 Poggio 以及 Zitnick 和 Kanade 採用了合作的匹配框架，試圖通過多個特徵的匹配信息以及唯一性假設來解決歧義。更好的方法是採用全局的方法進行求解，把多個像素或特徵的視差求解歸一到一個能量框架下。使用了能量最佳化的框架之後，能量函式的定義和最佳化變成了兩個較為獨立的問題，可以分別加以研究和解決。在定義能量函式方面，不同的算法採用不同的匹配信息和不同的先驗假設來描述能量函式中的不同部分，通過這些假設把大量的特徵聯繫起來，聯合求解以消除歧義。在能量最佳化方法方面，較傳統的有模擬退火（Simulated Annealing）算法、最可靠有限算法等。近些年，基於圖切割（Graph-Cuts）和置信度傳遞（Belief-Propogation）的最佳化算法逐漸被廣泛採用。以上算法的速度都較慢，主要原因在於當平滑函式為一般函式的時候，以上的能量最佳化函式是一個 NP難題。為了提高效率，一些研究人員考慮採用具有低階多項式複雜度的動態規划算法，此時需要把最佳化局限於單條掃描線或把多連通的圖變成一棵樹。
問題描述
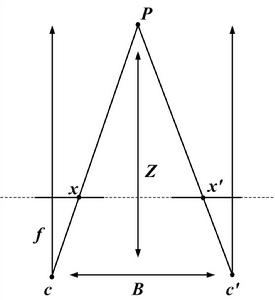圖 1：標準配置下雙目立體視覺的幾何模型和視差的定義。圖中 c 和 c' 分別為參考相機和匹配相機的光心， Z 為空間中點 P 的深度，B 為基線長度，視差定義為 P 點在兩相機中成像的水平坐標的差值 x - x'。立體視覺匹配問題的輸入為若干不同視角的相機採集的圖像，輸出是這些圖像上的點的對應關係。圖 1 為標準配置下雙目立體視覺的幾何模型。c 和 c' 為兩相機的光心，f 為焦距，B 為兩光心的連線，也稱為基線，過光心且垂直於成像平面的直線稱為光軸。所謂標準配置是指兩個相機的光軸垂直於基線且互相平行。設兩相機的焦距相等，且相機的坐標系的水平坐標與基線方向平行，則空間中的點 P 在兩相機上成的像具有相同的豎直坐標，這個特點也叫立體視覺的外極線（EpipolarLine）(所謂的外極線是指外極平面和圖像平面的交線，其中外極平面是包含兩個焦點和空間點的平面)約束。對於一般配置的相機（如圖 2），通過相機標定和配準，可以得到標準配置下的圖像。如無特殊說明，本文餘下的部分所涉及的立體匹配問題，都是建立在標準配置下的幾何模型。
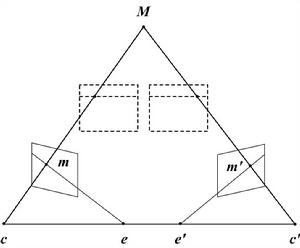
圖 2：一般位置的相機的立體成像幾何模型。通過相機的標定和配準，我們可以得到標準配置下的圖像，如圖中的虛線所示。圖中的~$c$~和~$c'$~為左右相機的光心，e 和 e' 稱為外極點，M 為三維空間中的一點，m 和 m' 分別為 M 在兩相機上的成的像。
設 P 點投影到兩相機後的圖像分別為 x 和 x'，我們說 x 和 x' 是一對對應點。如果我們用 x 和 x' 來表示它們的水平坐標，這兩個點的對應關係可以由如下定義的視差來描述：
d=x-x'
通過簡單的幾何關係推導，我們可以得到如下等式：
d= Bf / Z
可見當基線和焦距固定的時候，也就是相機的參數以及相機之間的相對位置和姿態固定不變的時候，視差與空間的點的深度成反比。因此，只需要知道了視差就可以得到物體的深度，從而立體視覺匹配問題可以定義為根據來自於不同的相機的圖像求解視差的問題。
