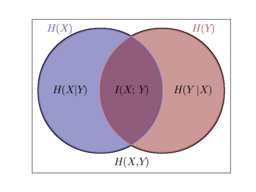
定義
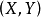互信息設兩個隨機變數
的聯合分布為
，邊際分布分別為
，互信息
是聯合分布
與乘積分布
的相對熵，即
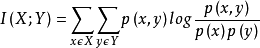互信息含義
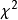互信息互信息與多元對數似然比檢驗以及皮爾森
校驗有著密切的聯繫。
信息的含義
信息是物質、能量、信息及其屬性的標示。逆維納信息定義
信息是確定性的增加。逆香農信息定義
信息是事物現象及其屬性標識的集合。
互信息的含義
一般而言，信道中總是存在著噪聲和干擾，信源發出訊息x，通過信道後信宿只可能收到由於干擾作用引起的某種變形的y。信宿收到y後推測信源發出x的機率，這一過程可由後驗機率p(x|y)來描述。相應地，信源發出x的機率p(x)稱為先驗機率。我們定義x的後驗機率與先驗機率比值的對數為y對x的互信息量（簡稱互信息）。
根據熵的連鎖規則，有
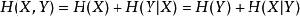互信息因此，
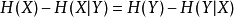互信息這個差叫做X和Y的互信息，記作I(X;Y)。
按照熵的定義展開可以得到：
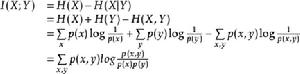互信息性質
非負性
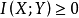互信息，且等號成立的充要條件是
和
相互獨立。
鏈法則
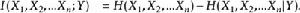互信息數據處理不等式
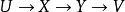互信息如果
構成馬式鏈，則
其他
某個詞t和某個類別Ci傳統的互信息定義如下:
互信息是計算語言學模型分析的常用方法，它度量兩個對象之間的相互性。在過濾問題中用於度量特徵對於主題的區分度。互信息的定義與交叉熵近似。互信息本來是資訊理論中的一個概念,用於表示信息之間的關係, 是兩個隨機變數統計相關性的測度，使用互信息理論進行特徵抽取是基於如下假設:在某個特定類別出現頻率高,但在其他類別出現頻率比較低的詞條與該類的互信息比較大。通常用互信息作為特徵詞和類別之間的測度，如果特徵詞屬於該類的話，它們的互信息量最大。由於該方法不需要對特徵詞和類別之間關係的性質作任何假設，因此非常適合於文本分類的特徵和類別的配準工作。
