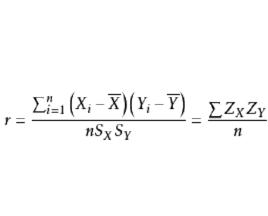基本介紹
積差相關(Pearson Product Moment Correlation Coefficient)是Pearson建立起來的、套用最廣泛的相關分析技術。它以相關係數的形式較為準確地反應了兩個變數之間的線性相關程度。一般來說,用積差相關計算相關係數的數據要滿足以下條件:
(1)兩個變數都是由測量獲得的連續型數據;
(2)兩個變數的總體都是呈常態分配,或接近常態分配,至少是單峰對稱分布;
(3)必須是成對的數據,即兩個變數應來自對同一總體或樣本的測量;
(4)兩個變數之間呈線性關係;
(5)大樣本,n≥30 。
相關係數的計算
協方差(covariance)是積差相關係數的基礎。協方差表示兩個隨機變數在多大程度上擁有相同的方差,是兩個變數的離差乘積之和除以n所得之商。其計算公式如下:
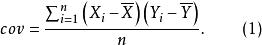 積差相關
積差相關 積差相關
積差相關當X與Y存在嚴格的線性關係時,數據的協方差可能達到最大值;當X與Y之間沒有關係或它們的關係不能用一條直線來描述時,協方差等於0。協方差本身沒有實際的意義,將它作為一個描述性的統計量,除以兩個變數的標準差,便可算得相關係數:
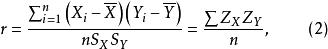 積差相關
積差相關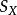 積差相關
積差相關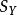 積差相關
積差相關其中,是變數X的標準差,是變數Y的標準差。
 積差相關
積差相關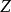 積差相關
積差相關 積差相關
積差相關 積差相關
積差相關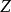 積差相關
積差相關從公式2也可看出,其實就是兩個隨機變數的標準分數相乘後累加,最後再除以n。這正好說明了含義,一個較大的值說明每一個個體或者事件在兩個隨機變數上獲得大約相等值,也就是X和Y變數在各自的分布中大致位於相同的位置。
注意點:
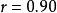 積差相關
積差相關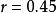 積差相關
積差相關(1) 相關係數不是等距或等比變數,它是順序變數。因此它只能比較大小,但不能直接做加、減、乘、除運算。比如,不能認為的相關強度是的兩倍,或者直接進行加減運算。
(2) 相關係數反映了變數間共變關係的密切程度,介於-1到1之間。正負號代表相關的性質,絕對值大小則反映了變數間的相關程度 。
相關係數的顯著性檢驗
 積差相關
積差相關 積差相關
積差相關 積差相關
積差相關相關係數的顯著性檢驗的目的是用樣本相關係數推斷總體是否相關。由於相關係數是根據樣本數據計算出來的,它會受到樣本波動的影響。能否根據樣本相關係數來說明總體的相關係數呢?這就需要考察樣本相關係數的可靠性,也就是進行顯著性檢驗。
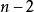 積差相關
積差相關 積差相關
積差相關就Pearson相關係數來說,它符合自由度為的分布,該檢驗可用於小樣本,也可用於大樣本,檢驗的具體步驟如下:
第1步:提出假設:
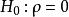 積差相關
積差相關即總體相關係數等於0;
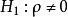 積差相關
積差相關即總體相關係數不等於0。
第2步:計算檢驗的統計量:
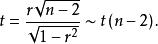 積差相關
積差相關第3步:進行決策。
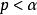 積差相關
積差相關 積差相關
積差相關求出統計量的p值,如果,則拒絕,表明總體的兩個變數之間存在顯著的線性關係 。