定義
若用(x，y)，i=1，2，…，n，表示兩個變數的等級，則此時的相關係數稱為斯皮爾曼等級相關係數。常被套用於測驗分數統計中。相關分析方法之一。由英國心理學家、統計學家斯皮爾曼根據積差相關的概念推導得出。它適用於只有兩列變數，且屬於等級變數性質的具有線性關係的數據資料。它的適用範圍要寬於積差相關。
公式
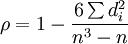斯皮爾曼等級相關n為等級個數
d為二列成對變數的等級差數
套用
假設當前有5個人的視覺、聽覺反應時（單位：毫秒），數據如下表。請問視覺、聽覺反應時是否具有一致性？
| 被試 | 聽覺反應時 | 視覺反應時 | X | Y | d | d^2 | XY |
| 1 | 170 | 180 | 3 | 4 | -1 | 1 | 12 |
| 2 | 150 | 165 | 1 | 1 | 0 | 0 | 1 |
| 3 | 210 | 190 | 5 | 5 | 0 | 0 | 25 |
| 4 | 180 | 168 | 4 | 2 | 2 | 4 | 8 |
| 5 | 160 | 172 | 2 | 3 | -1 | 1 | 6 |
| ∑ | 870 | 875 | 15 | 15 | 6 | 52 |
解：此題被試5人，不知是否為常態分配，所以用斯皮爾曼等級相關解題。其中，x為聽覺反應時間按大小排序，y為視覺反應時間按大小排序。d=x-y。
將n=5，∑d^2=6 帶入公式 1-[6·∑(di)^2 / (n^3 - n)]
得：ρ=0.7
答：這5人的視聽反應時等級相關係數為0.7，屬於高度相關。
優缺點
優點
適用範圍廣泛，斯皮爾曼等級相關對數據條件的要求沒有積差相關係數嚴格，只要兩個變數的觀測值是成對的等級評定資料，或者是由連續變數觀測資料轉化得到的等級資料，不論兩個變數的總體分布形態、樣本容量的大小如何，都可以用斯皮爾曼等級相關來進行研究。
缺點
一組能用積差相關計算的數據，如果改用等級相關，精確度會低於積差相關。凡符合積差相關條件的，最好不要用等級相關計算。
注意事項
在使用斯皮爾曼等級相關時，需要注意的有：
若非等距的連續變數因為分布不明，可用等級相關/也可用Pearson相關，對於完全等級離散變數必用等級相關；
當資料不服從雙變數常態分配或總體分布未知或原始數據是用等級表示時，宜用Spearman 相關；
若不恰當用了等級相關，可能得相關係數偏小或偏大結論而考察不到不同變數間存在的密切關係。對一般情況默認數據服從常態分配的，故用Pearson分析方法。
1.若非等距的連續變數因為分布不明，可用等級相關/也可用Pearson相關，對於完全等級離散變數必用等級相關；
2.當資料不服從雙變數常態分配或總體分布未知或原始數據是用等級表示時，宜用Spearman 相關；
3.若不恰當用了等級相關，可能得相關係數偏小或偏大結論而考察不到不同變數間存在的密切關係。對一般情況默認數據服從常態分配的，故用Pearson分析方法。
