二列相關的公式
例如學生成績是連續變數(0~100),某一道題給分也是連續的(0~6),現在把這題得分超過3分的算作一類,低於3分的算作另一類,就得到了二列相關。二列相關的係數就是這道題的區分度。
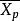 二列相關
二列相關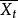 二列相關
二列相關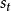 二列相關
二列相關其中代表此題超過3分的學生的平均總分,代表所有學生的平均總分,代表全體學生的總分的標準差,p是超過3分的學生占的比例,y是常態分配中與p對應的縱高。
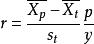 二列相關
二列相關需要注意的是,y值需要查表得出,統計軟體可能沒有根據p值自動計算y值的函式。
實際套用中可以直接把這道題的原始得分與總分做回歸,而不必要人為劃分成二列相關。
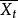 二列相關
二列相關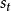 二列相關
二列相關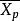 二列相關
二列相關既然可以用原始數據做積差相關,為什麼要人為劃分為二列相關呢?因為:1人工計算而言,二列相關更簡單,只需要算一個平均值、一個比例值p、一個標準差,另一個平均值可以從前面的和p求出;2二列相關描述足夠清楚。
二列相關的使用條件
二列相關的使用條件是:
1、兩列變數都是連續變數,總體呈常態分配,或接近常態分配,至少是單峰對稱分布。
2、兩變數之間是線性關係。
3、二分變數是人為劃分的,分界點應儘量靠近中值。
4、樣本容量應大於80。
例如學生成績是連續變數(0~100),某一道題給分也是連續的(0~6),現在把這題得分超過3分的算作一類,低於3分的算作另一類,就得到了二列相關。二列相關的係數就是這道題的區分度。
但是,如果是一道是非題,給分是有兩檔,就不是二列相關,而是點二列相關。
一般而言主觀題的區分度比選擇題高,如果把二列相關當成點二列相關,就低估了主觀題的區分度;反之,把是非題當做二列相關計算,會高估題目的區分度。
點二列相關
點二列相關的一列變數是連續變數(等距或等比變數),另一列是真實二分稱名變數(如男和女,對與錯等),與二列相關有區別。點二列相關可以直接由皮爾遜積差相關推導而來(詳見參考文檔) ,而二列相關的推導複雜得多。
二列相關的要求更精確(常態分配),計算得到的相關係數也大於點二列相關。
