程式驗證
正文
研究程式正確性的理論。為了解一個程式是否正確地實現了預定的目標,通常是規定一些初始數據,試驗性地執行這個程式,測試其是否能產生所要的答案。如果發現有誤,就檢查和修改所編的程式,直至對所有規定的初始數據,都能產生預期的結果。這種方法稱為程式調試。但是,程式對不同的初始數據的加工過程是不同的,而初始數據的取值範圍往往又十分廣泛。因此,使用調試方法窮盡程式的各種可能加工過程以確保程式的正確性,幾乎是不可能實現的。因此,調試方法只能發現程式的錯誤,而不能確保程式無誤。程式驗證則是研究如何使用數學方法嚴格證明一個程式是符合其預定的目標的,因而是正確無誤的。發展概況 美籍匈牙利科學家J.諾伊曼於1947年發表的論文中就提到程式正確性證明。美國科學家R.W.弗洛依德於1967年系統地提出驗證程式正確性的歸納斷言方法,引起了計算機科學界研究程式驗證的熱潮。英國科學家C.A.R.霍爾於1969年將歸納斷言方法形式化,提出程式驗證的公理系統。1969年以來又陸續出現很多使用歸納斷言方法或者結構歸納法的自動程式驗證系統,其中以70年代中期實現的波伊爾-莫爾程式驗證系統最為著名。70年代以來還出現能輔助用戶正確編製程序的實用的半自動化程式驗證系統。在使用這種系統時,用戶必須協助系統完成程式驗證中創造性最強的部分工作。
基本方法 下面的框圖代表一個非負整數的除法程式。x1是被除數;x2是除數;z1中存放程式加工後得到的商;z2中存放得到的餘數;y1、y2是程式加工時使用的工作單元。START 表示程式的起始,HALT表示程式的終止。方框中是同時賦值語句,如
(y1,y2):=(O,x1)
表示將y1置0值的同時,將y2的值置為x1。圓框內是測試語句,用於控制程式加工的流程。如框圖中的語句y2≥x2
表示當y2的值大於等於x2時,程式按yes的箭頭繼續執行;否則按no的箭頭繼續執行。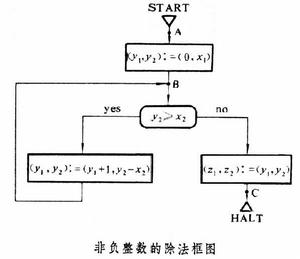 程式驗證
程式驗證若約定各個變數的取值都是整數,上述除法程式的輸入謂詞和輸出謂詞分別為
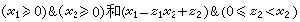
在除法程式中設定三個斷言,A處和C處的斷言分別為上述輸入和輸出謂詞,B處斷言為
(x1=y1x2+y2)&(y2≥0) (1)
反映了y1、y2中存放商數和餘數的中間結果值。驗證程式的正確性,就是證明在程式的任何一種可能的加工過程中所設定的斷言都是成立的。程式的一個加工過程就是框圖中的一個流程。除法程式的所有可能的流程都是由圖上的三條路徑組合而成:由A至B;由B出發回到B;由B至C。這樣,驗證程式的正確性,就是證明對任一條路徑,只要起點的斷言成立,則終點的斷言也成立。
以第二條路徑為例,它是一條環路。要證明下列命題:若程式執行到環路的起點B時,斷言(1)成立,則程式執行一周,再達到B點時,斷言(1)仍然成立。
環行該圈,就是在(y2≥x2)成立的條件下,執行賦值語句
(y1,y2):=(y1+1,y2-x2)
而上述語句的執行結果是使 y1的取值為執行前y1的值加1,y2的取值為執行前y2的值與x2的差,其他變數的值不變。為保證執行該賦值語句後斷言(1)仍然成立,就要求將斷言(1)中的y1代為(y1+1),y2代為(y2-x2)後得到的公式在執行該語句前成立。即(x1=(y1+1)x2+(y2-x2))&(y2-x2≥0) (2)
在執行上述賦值語句前成立。但已知執行該語句前斷言①和測試條件(y2≥x2)均成立。由此推斷公式②是成立的。這樣就完成了對第二條路徑的驗證。對其餘兩條路徑的驗證也是類似的。從而可以證明除法程式的正確性。歸納斷言方法是由建立斷言和對各條路徑逐條驗證兩部分組成的。建立斷言是一種創造性的工作,而驗證路徑的工作儘管繁瑣,卻是機械的。如何由計算機系統協助用戶歸納出合適的斷言,是程式驗證研究中的重要課題。
用上述方法只能證明在輸入謂詞成立的前提下,程式終止時輸出謂詞一定成立。但不能證明在輸入謂詞成立時,程式一定能終止。不討論程式終止性的程式驗證稱為程式部分正確性的驗證。包括終止性的驗證,則稱為程式完全正確性的驗證。
程式驗證技術除了用於證明程式的正確性,或輔助用戶編制正確程式外,還可從程式正確性角度評價程式設計方法和程式設計語言的優劣。但是,保證程式正確性的有效辦法,不是在編製程序後再去驗證,而是設法在編制過程中,使用適當的技術,使產生的程式是正確無誤的。這類技術叫作程式綜合和程式變形。程式驗證技術和程式綜合變形技術相互參照,共同發展。