公理語義學
正文
形式語義學的一個分支。不同的人在了解程式的含義時有不同的要求。公理語義學方法就是研究如何將這些不同的要求形式化,並根據這些要求嚴格給出程式設計語言的有關語義。1967年美國R.W.弗洛依德提出描述人們所關心的程式含義,以及如何去論證一個程式是否具有某種含義的數學方法。1969年英國C.A.R.霍爾首次用公理系統定義了一類程式設計語言的語義。1975年荷蘭E.W.戴克斯特拉提出基於最弱前置條件的公理語義學描述方法,成為程式設計方法學的一個基本概念。
基本方法 在定義語言的公理語義時,必須先給出描述所關心的程式語義的形式化方法,然後建立公理系統,規定語言成分的有關語義。如果用一個程式P去計算自然數的階乘,這個程式中的變數x在程式開始執行時,存放用戶輸入的自然數值κ;而在程式執行終止時,存放要輸出的結果。用戶關心的是程式P計算的結果值是否確是輸入值的階乘。在公理語義學中,使用公式{x=κ}P{x=κ!}表示程式P的這一部分含義:若P執行前x的值等於κ,則P執行完畢後 x的值等於κ!。程式P執行前的條件(x=κ)稱為P的前置條件,執行後的條件(x=κ!)稱為P的後置條件。這類公式稱為歸納命題。一般地說,歸納命題{R}P{Q}表示:若程式P執行前,其程式變數的值滿足前置條件R,則程式P執行完畢後,其程式變數的值滿足後置條件Q。歸納命題用來作為描述程式有關語義的工具,公理語義學就是用歸納命題的公理系統來定義程式語言的語義。
執行賦值語句(x:=e)的結果是將程式變數x 的值變為執行該語句前表達式e的值。也就是說,執行該語句後x的值等於執行該語句前表達式e的值。因此,若表達式e在語句(x:=e)執行前滿足條件R,那么程式變數x在語句(x:=e)執行完畢後亦應滿足條件R。故歸納命題{R【e/x】}x:=e{R}應該永遠成立。其中R【e/x】成立,表示將R中的x代為e後,R成立,即e滿足R。在公理系統中,公理是一種永遠成立的命題。這樣採用{R【e/x】} x:=e{R}作為公理,就表達了語句(x:=e)的語義,使用不同的R,可反映不同的用戶對賦值語句語義的要求,R可以只涉及輸入輸出變數;也可以涉及工作單元,用來表達賦值語句的副作用。
執行順序語句(s1;s2),就是使用執行(s1;s2)前程式變數的值,先執行s1,然後使用執行s1後程式變數的結果值,再執行語句s2,s2執行完畢後的程式變數值,就是執行順序語句(s1;s2)的結果值。故若執行(s1;s2)前的程式變數值滿足條件R,(s1;s2)執行完畢後的值滿足T,那么就可找到關於中間結果的條件Q,使得若R為s1的前置條件,則Q為s1的後置條件,而且以Q為s2的前置條件,則T就是s2的後置條件,這樣就可以採用推理規則
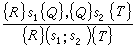
其他語言成分的公理語義也是用公理和推理規則類似地給出,但有的成分(如過程調用等)的語義,比起上述語句的語義要複雜得多。
研究方向 論證一個程式是否具有某種含義的過程和論證一個程式是否具有某種特性的過程是完全一致的。故公理語義學是程式正確性研究的理論基礎。程式驗證的研究也進一步促進公理語義學的發展。
尋求適用於描述程式語義,且便於語義推導的邏輯語言是公理語義學研究的一個重要方面。70年代末出現了使用時態邏輯來定義語言的語義,稱為時態語義。另外如動態邏輯、算法邏輯在語義學中的套用,也都在發展之中。