簡介
為簡化磁場的計算,在一定條件下,引入的一個輔助物理量。
原理
如果穩恆磁場的某個局部區域V中沒有傳導電流,且其中任何封閉曲線L都不能包圍傳導電流,以H表示區域內各點的磁場強度,ds表示面積元,即有
 (1)
(1)
H=-墷嗞m。 (2)
取V中某點Po作為基準點,定義任一點P的磁標勢嗞m(P)如下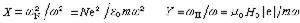 (3)
(3)
式(2)中嗞m(Po)為任一常數,H的單位是安/米,嗞m的單位是安。
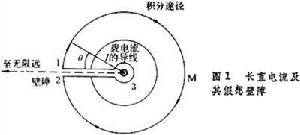
穩恆電流大都是在細長導線的迴路中流動的。磁場則大都在沒有傳導電流的空間中。為了使 V中的任一封閉曲線滿足式(1),可限定以電流迴路為邊緣的任意形狀的一個曲面為不可穿越的壁障。圖1、圖2分別示出了長直電流和圓形電流所假想的壁障。其中長直電流的壁障是包含電流且向左延伸的無窮大平面,圖1中的1與2是壁障二側無限靠近的二點。套用安培環路定理求H的環量時,如取途徑1M231不包圍電流,可使式(1)滿足。當取由1經M至2的途徑對H積分時,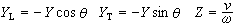 值等於長直電流的電流強度I。由式(3)得
值等於長直電流的電流強度I。由式(3)得
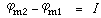 (4)
(4)
 磁標勢
磁標勢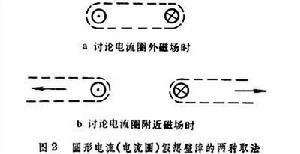 磁標勢
磁標勢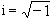 。
。
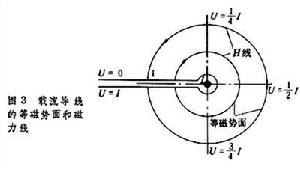 磁標勢
磁標勢 (5)
(5)
式中I是迴路中的電流,Ω是迴路在P點所張的立體角,從P點看電流逆時針方向時,立體角為正。如果計算出立體角Ω,再根據式(2)即得H。
在討論磁介質磁化或鐵磁體的磁場時,因所討論磁場範圍內沒有傳導電流,故可用磁標勢法來處理。
由磁場的高斯定理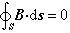 和H的定義
和H的定義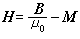 可得H的高斯定理
可得H的高斯定理
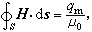 (6)
(6)
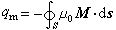 (7)
(7)
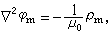 (8)
(8)
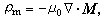 (9)
(9)
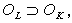 (10)
(10)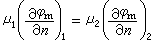 (11)
(11)