相關定義
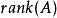 矩陣的秩
矩陣的秩方陣(行數、列數相等的矩陣)的列秩和行秩總是相等的,因此它們可以簡單地稱作矩陣 A的 秩。通常表示為r( A),rk( A)或。
m × n矩陣的秩最大為 m和 n中的較小者,表示為 min( m, n)。有儘可能大的秩的矩陣被稱為有 滿秩;類似的,否則矩陣是 秩不足(或稱為“ 欠秩”)的。
設A是一組向量,定義A的極大無關組中向量的個數為A的秩。
定義1. 在m*n矩陣A中,任意決定k行和k列交叉點上的元素構成A的一個k階子矩陣,此子矩陣的行列式,稱為A的一個k階子式。
例如,在階梯形矩陣中,選定1,3行和3,4列,它們交叉點上的元素所組成的2階子矩陣的行列式 就是矩陣A的一個2階子式。
定義2. A=(aij)m×n的不為零的子式的最大階數稱為矩陣A的秩,記作rA,或rankA或R(A)。
特別規定零矩陣的秩為零。
顯然rA≤min(m,n) 易得:
若A中至少有一個r階子式不等於零,且在r<min(m,n)時,A中所有的r+1階子式全為零,則A的秩為r。
由定義直接可得n階可逆矩陣的秩為n,通常又將可逆矩陣稱為滿秩矩陣, det(A)≠0;不滿秩矩陣就是奇異矩陣,det(A)=0。
由行列式的性質1(1.5[4])知,矩陣A的轉置AT的秩與A的秩是一樣的。
矩陣的秩
引理 設矩陣A=(aij)sxn的列秩等於A的列數n,則A的列秩,秩都等於n。
定理 矩陣的行秩,列秩,秩都相等。
定理 初等變換不改變矩陣的秩。
定理 矩陣的乘積的秩Rab<=min{Ra,Rb};
當r(A)<=n-2時,最高階非零子式的階數<=n-2,任何n-1階子式均為零,而伴隨陣中的各元素就是n-1階子式再加上個正負號,所以伴隨陣為0矩陣。
當r(A)<=n-1時,最高階非零子式的階數<=n-1,所以n-1階子式有可能不為零,所以伴隨陣有可能非零(等號成立時伴隨陣必為非零)。
變化規律
(1)轉置後秩不變
(2)r(A)<=min(m,n),A是m*n型矩陣
(3)r(kA)=r(A),k不等於0
(4)r(A)=0 <=> A=0
(5)r(A+B)<=r(A)+r(B)
(6)r(AB)<=min(r(A),r(B))
(7)r(A)+r(B)-n<=r(AB)
證明:
AB與n階單位矩陣En構造分塊矩陣
|AB O|
|O En|
A分乘下面兩塊矩陣加到上面兩塊矩陣,有
|AB A|
|0 En|
右邊兩塊矩陣分乘-B加到左邊兩塊矩陣,有
|0 A |
|-B En|
所以,r(AB)+n=r(第一個矩陣)=r(最後一個矩陣)>=r(A)+r(B)
即r(A)+r(B)-n<=r(AB)
註:這裡的n指的是A的列數。這裡假定A是m×n matrix。
特別的:A:m*n,B:n*s,AB=0 -> r(A)+r(B)<=n
(8)P,Q為可逆矩陣, 則 r(PA)=r(A)=r(AQ)=r(PAQ)

