定義
 矩量母函式
矩量母函式 矩量母函式
矩量母函式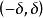 矩量母函式
矩量母函式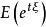 矩量母函式
矩量母函式定義1(矩量母函式)設 為隨機變數,若存在某正實數 ,使得對於區間 中任一實數t,數學期望 均存在,則稱
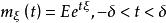 矩量母函式
矩量母函式 矩量母函式
矩量母函式為隨機變數 或其分布的 矩量母函式(moment generating function),簡記為mgf.
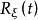 矩量母函式
矩量母函式另外,稱矩量母函式的對數為累積量生成函式。
與特徵函式的聯繫
 矩量母函式
矩量母函式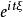 矩量母函式
矩量母函式定義2(特徵函式)設 為隨機變數,稱復隨機變數 的數學期望
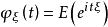 矩量母函式
矩量母函式 矩量母函式
矩量母函式為 的特徵函式,其中t為實數。
特徵函式具有以下性質:
(1)如果兩個隨機變數具有相同的特徵函式,那么它們具有相同的機率分布; 反之, 如果兩個隨機變數具有相同的機率分布, 它們的特徵函式也相同(顯然)。
(2)獨立隨機變數和的特徵函式等於每個隨機變數特徵函式的乘積。
 矩量母函式
矩量母函式綜合定義1和定義2,可得隨機變數 的特徵函式與其mgf之間存在如下關係:
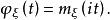 矩量母函式
矩量母函式對比特徵函式的性質,隨機變數的mgf也具有如下常用性質:
(1)如果兩個隨機變數具有相同的mgf,那么它們具有相同的機率分布; 反之, 如果兩個隨機變數具有相同的機率分布, 它們的mgf也相同。(即在mgf存在的情況下,隨機變數的mgf與其機率分布相互唯一確定。)
(2)獨立隨機變數和的mgf等於每個隨機變數mgf的乘積。
性質
 矩量母函式
矩量母函式以連續隨機變數為例,離散型隨機變數可做相同變換。
(1)由泰勒級數
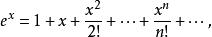 矩量母函式
矩量母函式有
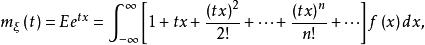 矩量母函式
矩量母函式即
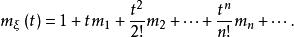 矩量母函式
矩量母函式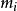 矩量母函式
矩量母函式 矩量母函式
矩量母函式其中, 是隨機變數 的i階中心矩。
(2)m(-t)是雙側拉普拉斯變換(Laplace Transform)。
(3)不管機率分布是不是連續,矩量母函式都可以用黎曼-斯蒂爾切斯積分給出:
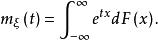 矩量母函式
矩量母函式其中,F(x)是累積分布函式(Cumulative Distribution Function, 簡稱CDF)。
套用
常見分布的mgf
 矩量母函式
矩量母函式對於隨機變數,有如下結論:
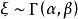 矩量母函式
矩量母函式 矩量母函式
矩量母函式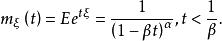 矩量母函式
矩量母函式(1)若,則的mgf為
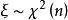 矩量母函式
矩量母函式 矩量母函式
矩量母函式(2)若,則的mgf為
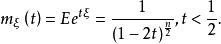 矩量母函式
矩量母函式 矩量母函式
矩量母函式 矩量母函式
矩量母函式 矩量母函式
矩量母函式(3)若服從參數為的指數分布,則的mgf為
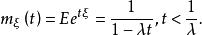 矩量母函式
矩量母函式求隨機變數的矩
 矩量母函式
矩量母函式 矩量母函式
矩量母函式 矩量母函式
矩量母函式設隨機變數 的矩量母函式存在,則 的各階矩存在且可由矩量母函式表示。具體地, 的k階矩為矩量母函式在0點的k階導數值,即對任意正整數k,有
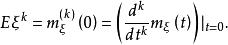 矩量母函式
矩量母函式特別地,有
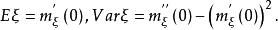 矩量母函式
矩量母函式證明:由泰勒級數
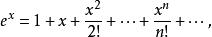 矩量母函式
矩量母函式有
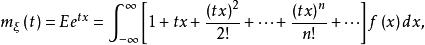 矩量母函式
矩量母函式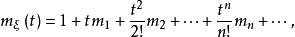 矩量母函式
矩量母函式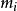 矩量母函式
矩量母函式 矩量母函式
矩量母函式即其中,是隨機變數的i階中心矩。上式左右兩邊同時對t求n階導,得到
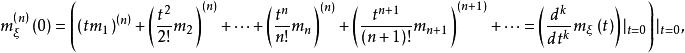 矩量母函式
矩量母函式故
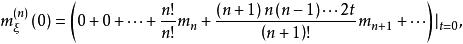 矩量母函式
矩量母函式即
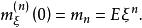 矩量母函式
矩量母函式證畢。

