特徵函式

在機率論中，任何隨機變數的特徵函式(縮寫：ch.f,複數形式：ch.f's)完全定義了它的機率分布。復隨機變數本質上是二維隨機變數，相關的很多概念和性質可以從實隨機變數直接推廣而得到，例如Eξ具有與實數學期望類似的性質.為ξ的特徵函式(Characteristic function)，這裡t是任意實數.它就是函式p(x)的傅立葉變換.

定義定律

定義1設ξ、η為實值隨機變數，稱ζ= ξ+ iη為復隨機變數，這裡i^2＝-1，稱Eζ=Eξ+Eiη為ζ的數學期望.

復隨機變數本質上是二維隨機變數，相關的很多概念和性質可以從實隨機變數直接推廣而得到，例如Eξ具有與實數學期望類似的性質.

定義2設為實隨機變數，稱

f(t)=Ee^(itξ)

(1)

為ξ的特徵函式(Characteristic function)，這裡t是任意實數.

由於E|e^(itξ)|=1, 因此對任意ξ，對一切t∈(--∞,∞)，(1)式都有意義. 換句話說，對每個隨機變數ξ（或者說每個分布函式F(x)），都有一個特徵函式f (t)與之對應，它是定義在(--∞,∞)上的實變數復值函式.

特徵函式是ξ的函式e^(itξ)的數學期望，故由§1得:

特徵函式

特別，若ξ為離散型，P(ξ=xn)=pn,n =1,2,…, 則

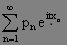特徵函式

f(t)=

(2)

若ξ是連續型，其密度為p (x)，則

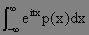特徵函式

f(t)=

(3)

它就是函式p(x)的傅立葉變換.