定義
單變數情形
如果 X是在非負整數域{0,1, ...}上取值的離散隨機變數,那么 X的機率母函式定義為 :
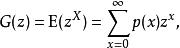 機率母函式
機率母函式其中 p是 X的機率質量函式。
多變數情形
如果 X= ( X,..., X )是在 d-非負整數格{0,1, ...}上取值的離散隨機變數, 那么 X的機率母函式定義為:
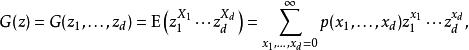 機率母函式
機率母函式其中 p是 X的機率質量函式。
性質
冪級數
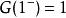 機率母函式
機率母函式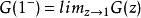 機率母函式
機率母函式機率母函式服從冪級數的所有非負係數的規則。特別地, ,其中 ,因為機率必須總和為1。所以任何機率母函式的收斂半徑必須至少為1,通過具有非負係數的冪級數的Abel定理來證明。
機率和期望
以下性質是與 X有關的各種基本量的推導:
1、X的機率質量函式通過取G的導數來恢復,
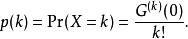 機率母函式
機率母函式2、機率密度函式的歸一化可以用母函式來表示:
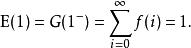 機率母函式
機率母函式該預期的 X由下式給出:
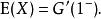 機率母函式
機率母函式所以, X的方差由下式給出 :
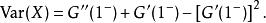 機率母函式
機率母函式獨立隨機變數的函式
機率母函式對於處理獨立隨機變數的函式特別有用。例如:
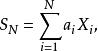 機率母函式
機率母函式如果 X, X,..., X是一系列獨立的(不一定是相同分布的)隨機變數,並且 其中a是常數,則機率母函式由下式給出:
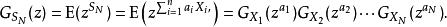 機率母函式
機率母函式例如,如果
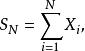 機率母函式
機率母函式那么,機率母函式 G( z)由下式給出:
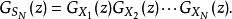 機率母函式
機率母函式也就是說,兩個獨立隨機變數 S= X- X的差的機率母函式是 :
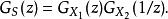 機率母函式
機率母函式示例
 機率母函式
機率母函式1.一個常數隨機變數(即 )的機率母函式是:
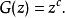 機率母函式
機率母函式2.一個的機率母函式二項式隨機變數,在成功的次數 Ñ試驗中,機率 p是每次試驗成功的機率,機率母函式是:
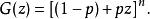 機率母函式
機率母函式注意,這是具有參數 p的伯努利隨機變數的機率母函式的 n倍乘積。
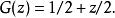 機率母函式
機率母函式所以,擲硬幣時間的機率母函式是:
3.一個機率母函式的負二項隨機變數在{0,1,2 ...}中,每次試驗的成功機率 p,機率母函式是 :
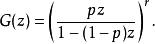 機率母函式
機率母函式相關概念
機率母函式是一個的例子母函式的序列組成:也見形式冪級數。這與機率質量函式的z變換等效,有時稱為z變換。
其他隨機變數的母函式包括矩母函式、特徵函式和累積量母函式。
