簡介
定義
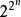 真值函式
真值函式真值函式亦稱真值函項。一種特殊函式。指以真值集 {T,F} 為定義域和值域的函式。根據真值函式的變元個數,真值函式可為一元真值函式,二元真值函式······ n 元真值函式等。對任意的自然數 n≥1,總有個不同的 n 元真值函式。
真值函式採用來自 {T,F} (就是真實和虛假) 的真值。例如句子 A → B 生成真值函式 h(A,B),它的真值是 F,若且唯若 A 的值是 T 而 B 的值是 F。n 個變數的命題句子生成 2 個真值函式,其中函式值為真的有 2 個。比如,如果有像 A → (B→A) 這樣的 2 個變數的命題則有 8 個生成的真值函式,其中函式值為真的有 4 個。函式值為真的真值函式組成一個句子的真值表。
陳述或命題被稱為是 真值泛函的,如果它的真值由它的部件的真值來決定。
例子
比如,“在2004年4月20日保羅·馬丁是加拿大首相”是真的,“在2004年4月20日喬治·沃克·布希是美國總統”也是真的,所以合取:“在2004年4月20日保羅·馬丁是加拿大首相 與 喬治·沃克·布希是美國總統”是真的。在這個句子中, “與”充當真值函式。相反的,在“在2004年4月20日阿爾·戈爾是美國總統”和“布蘭妮·斯皮爾斯相信在2004年4月20日阿爾·戈爾是美國總統”。知道前者不是真的和後者的真值之間沒有關係:布蘭妮·斯皮爾斯相信阿爾·戈爾是總統這個命題的真值,不是由阿爾·戈爾在那天 不是總統的事實來決定的。 所以,詞語“相信”不是真值函式。
其他解釋
用更加數學化的術語,真值函式是一種布爾函式,並使用布爾變數來持有真值函式的結果是計算機科學的普遍實踐。確定句子的真值是邏輯和數學二者的基本活動;作為結果,真值函式在與邏輯和數學基礎有關的著作中經常討論。
簡單真值函式如 AND、NOT 等可以用真值表確定。更複雜的真值函式可能需要重要的計算。
n元真值函式
n元函式就是有n個自變數的函式。 n元真值函式就是自變數和函式值都是真值(即0或1)的函式。
一元真值函式有4個,二元真值函式有8個,每個自變數有2個取值方式,n個自變數共有2 個不同取值方式。對n個自變數的每個取值方式,函式值有2個取值方式,即為0或1,故n元真值函式共有2*2 個。
例如,3元真值函式共有=256個。
一般地,函式F:{0,1}→{0,1}稱為n元真值函式,其中:{0,1}為{0,1}的卡氏積。