簡介
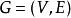 匈牙利算法
匈牙利算法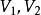 匈牙利算法
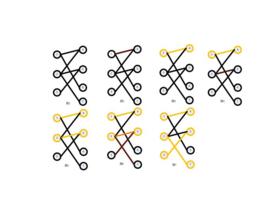
匈牙利算法設 是一個無向圖。如頂點集V可分割為兩個互不相交的子集 ,選擇這樣的子集中邊數最大的子集稱為圖的最大匹配問題(maximal matching problem)。
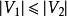 匈牙利算法
匈牙利算法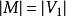 匈牙利算法
匈牙利算法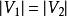 匈牙利算法
匈牙利算法如果一個匹配中, 且匹配數 ,則稱此匹配為完全匹配,也稱作完備匹配。特別的當 稱為完美匹配。
概念
在介紹匈牙利算法之前還是先提一下幾個概念,下面M是G的一個匹配。
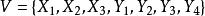 匈牙利算法
匈牙利算法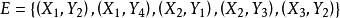 匈牙利算法
匈牙利算法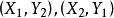 匈牙利算法
匈牙利算法若 , ,其中邊 已經在匹配M上。
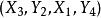 匈牙利算法
匈牙利算法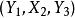 匈牙利算法
匈牙利算法M-交錯路:p是G的一條通路,如果p中的邊為屬於M中的邊與不屬於M但屬於G中的邊交替出現,則稱p是一條M-交錯路。如:路徑 , 。
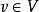 匈牙利算法
匈牙利算法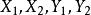 匈牙利算法
匈牙利算法M-飽和點:對於 ,如果v與M中的某條邊關聯,則稱v是M-飽和點,否則稱v是非M-飽和點。如 都屬於M-飽和點,而其它點都屬於非M-飽和點。
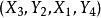 匈牙利算法
匈牙利算法M-可增廣路:p是一條M-交錯路,如果p的起點和終點都是非M-飽和點,則稱p為M-可增廣路。如 (不要和流網路中的增廣路徑弄混了)。
求最大匹配的一種顯而易見的算法是:先找出全部匹配,然後保留匹配數最多的。但是這個算法的時間複雜度為邊數的指數級函式。因此,需要尋求一種更加高效的算法。下面介紹用增廣路求最大匹配的方法(稱作匈牙利算法,匈牙利數學家Edmonds於1965年提出)。
增廣路的定義(也稱增廣軌或交錯軌):
若P是圖G中一條連通兩個未匹配頂點的路徑,並且屬於M的邊和不屬於M的邊(即已匹配和待匹配的邊)在P上交替出現,則稱P為相對於M的一條增廣路徑。
由增廣路的定義可以推出下述三個結論:
(1)P的路徑個數必定為奇數,第一條邊和最後一條邊都不屬於M。
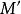 匈牙利算法
匈牙利算法(2)將M和P進行取反操作可以得到一個更大的匹配 。
(3)M為G的最大匹配若且唯若不存在M的增廣路徑。
算法輪廓:
(1)置M為空
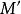 匈牙利算法
匈牙利算法(2)找出一條增廣路徑P,通過異或操作獲得更大的匹配 代替M
(3)重複(2)操作直到找不出增廣路徑為止
複雜度
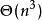 匈牙利算法
匈牙利算法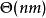 匈牙利算法
匈牙利算法時間複雜度鄰接矩陣:最壞為 鄰接表:
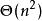 匈牙利算法
匈牙利算法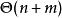 匈牙利算法
匈牙利算法空間複雜度 鄰接矩陣: 鄰接表:
樣例程式
格式說明
輸入格式:
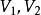 匈牙利算法
匈牙利算法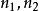 匈牙利算法
匈牙利算法第1行3個整數, 的節點數目 ,G的邊數m
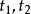 匈牙利算法
匈牙利算法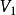 匈牙利算法
匈牙利算法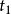 匈牙利算法
匈牙利算法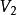 匈牙利算法
匈牙利算法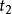 匈牙利算法
匈牙利算法第2-m+1行,每行兩個整數 ,代表 中編號為 的點和 中編號為 的點之間有邊相連
輸出格式:
1個整數ans,代表最大匹配數
鄰接矩陣-C
鄰接矩陣-pascal
鄰接表-pascal(使用動態鍊表)
(方法基於之前的鄰接矩陣-pascal)
鄰接表-C++
鄰接矩陣-C++