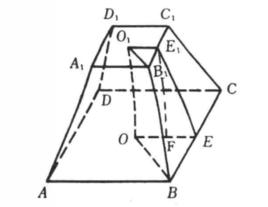
基本概念
用一個平行於稜錐底面的平面去截稜錐,介於底面和截面之間的部分叫做稜台(圖1)。其各部分的名稱如圖2所示。由正稜錐截得的稜台叫做 正稜台 。
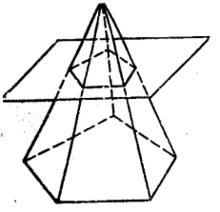 圖1 圖1 | 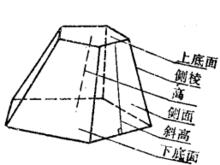 圖2 圖2 |
正稜台的主要性質
正稜台的主要性質有:
1.正稜台的兩底面以及平行於底面的截面是相似正多邊形;
2.各側棱都相等;
3.側面是全等的等腰梯形;
4.斜高都相等;
5.對角面是等腰梯形;
6.兩底面中心的連線垂直於底面;
7.各側棱和底面所成的角相等;
8.各側面和底面所成的二面角相等 。
正稜台的側面展開圖
正稜台的側面展開圖圖3(b)是由各個側面組成的平面圖形,它是由一些有公共頂點的等腰梯形組成的,這個公共頂點即為等腰梯形兩腰延長後的交點。等腰梯形的上、下底就是正稜台上、下底面邊長.等腰梯形的腰就是正稜台的側棱長。
正稜台的表面積
圖3是正稜台和它的側面展開圖,這個側面展開圖是由幾個全等的等腰梯形組成的,每個梯形的上底和下底分別是正稜台上底面和下底面多邊形的邊,兩腰是正稜台的側棱,設這個正稜台上、下底面周長分別是c'和c,斜高是h',我們有下面的定理 :
定理 正稜台的側面積等於它的兩個底面周長的和與斜高的乘積的一半,即
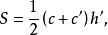 正稜台
正稜台其中,c、c'和h'分別表示正稜台的兩個底面周長和斜高。正稜台的全面積等於它的側面積與兩個底面積的和 。
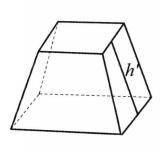 圖3(a)
圖3(a)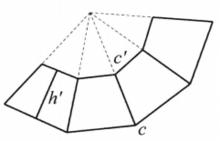 圖3(b)
圖3(b)正稜台的體積
設稜台的上底面積為S₁,下底面積為S₂,高為h,它的體積為V,則稜台的體積計算公式如下:
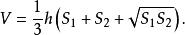 正稜台
正稜台稜台的體積等於這三個稜錐的體積之和:
1.以稜台的高作高,它的下底作底的;
2.以稜台的高作高,它的上底作底的;
3.以稜台的高作高,它的上下兩底面積的比例中項作底的 。