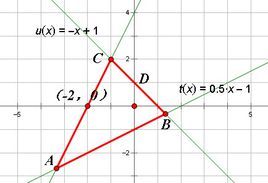
方程與等式
方程與等式的關係
方程一定是等式,但等式不一定是方程。
例子:a+b=13 符合等式,有未知數。這個是等式,也是方程。
1+1=2 ,100X100=10000。這兩個式子符合等式,但沒有未知數,所以都不是方程。
在定義中,方程一定是等式,但是等式可以有其他的,比如上面舉的1+1=2,100X100=10000,都是等式,顯然等式的範圍大一點。
解方程依據
1.:把方程中的某些項帶著前面的符號從方程的一邊移到另一邊,並且加變減,減變加,乘變除以,除以變乘;
2.等式的基本性質
性質1
等式兩邊同時加(或減)同一個數或同一個代數式,所得的結果仍是等式。用字母表示為:若a=b,c為一個數或一個代數式。則:(1) a+c=b+c (2) a-c=b-c
性質2
等式的兩邊同時乘或除以同一個不為0的數所得的結果仍是等式。
用字母表示為:若a=b,c為一個數或一個代數式(不為0)。則這個:
a×c=b×c a÷c=b÷c
性質3
若a=b,則b=a(等式的對稱性)。
性質4
若a=b,b=c則a=c(等式的傳遞性)。
3.合併同類項;
解方程步驟
1.能計算的先計算; 2.轉化——計算——結果
一元一次方程
只含有一個未知數,且未知數次數是一的整式方程叫一元一次方程(linear equation with one unknown)。通常形式是ax+b=0(a,b為常數,且a≠0)。
一般解法
去分母 方程兩邊同時乘各分母的最低公倍數。
去括弧 一般先去小括弧,再去中括弧,最後去大括弧。但順序有時可依據情況而定使計算簡便。可根據乘法分配律。
移項 把方程中含有未知數的項移到方程的另一邊,其餘各項移到方程的另一邊移項時別忘記了要變號。(一般都是這樣:(比方)從 5x=4x+8 得到 5x - 4x=8 ;把未知數移到一起!
合併同類項 將原方程化為ax=b(a≠0)的形式。
化係數為一 方程兩邊同時除以未知數的係數。
得出方程的解。
例如:
3x=5×6
解:3x=30
x=30÷3
x=10
教學設計
教學目標
使學生初步掌握一元一次方程解簡單套用題的方法和步驟;並會列出一元一次方程解簡單的套用題
培養學生觀察能力,提高他們分析問題和解決問題的能力
使學生初步養成正確思考問題的良好習慣.
重點難點
一元一次方程解簡單的套用題的方法和步驟.
教學過程
一、從學生原有的認知結構提出問題
在國小算術中,我們學習了用算術方法解決實際問題的有關知識,那么,一個實際問題能否套用一元一次方程來解決呢?若能解決,怎樣解?用一元一次方程解套用題與用算術方法解套用題相比較,它有什麼優越性呢?
為了回答上述這幾個問題,我們來看下面這個例題.
例1 某數的3倍減2等於某數與4的和,求某數.
(首先,用算術方法解,由學生回答,教師板書)
解法1:(4+2)÷(3-1)=3.
答:某數為3.
(其次,用代數方法來解,教師引導,學生口述完成)
解法2:設某數為x,則有3x-2=x+4.
3x-2=x+4
解:(3-1)x=2+4
2x=2+4
2x=6
x=6÷2
x=3
解之,得x=3.
答:某數為3.
縱觀例1的這兩種解法,很明顯,算術方法不易思考,而套用設未知數,列出方程並通過解方程求得套用題的解的方法,有一種化難為易之感,這就是我們學習運用一元一次方程解套用題的目的之一.
我們知道方程是一個含有未知數的等式,而等式表示了一個相等關係.因此對於任何一個套用題中提供的條件,應首先從中找出一個相等關係,然後再將這個相等關係表示成方程.
本節課,我們就通過實例來說明怎樣尋找一個相等的關係和把這個相等關係轉化為方程的方法和步驟.
二、師生共同分析、研究一元一次方程解簡單套用題的方法和步驟
例2 某麵粉倉庫存放的麵粉運出 15%後,還剩餘42500千克,這個倉庫原來有多少麵粉?
師生共同分析:
本題中給出的已知量和未知量各是什麼?
已知量與未知量之間存在著怎樣的相等關係?(原來重量-運出重量=剩餘重量)
若設原來麵粉有x千克,則運出麵粉可表示為多少千克?利用上述相等關係,如何布列方程?
上述分析過程可列表如下:
解:設原來有x千克麵粉,那么運出了15%x千克,由題意,得x-15%x=42500,
x-15%x=42500
解:(1-15%)x=42500
85%x=42500
x=42500÷85%
x=50000
所以 x=50000.
答:原來有 50000千克麵粉.
此時,讓學生討論:本題的相等關係除了上述表達形式以外,是否還有其他表達形式?若有,是什麼?
(還有,原來重量=運出重量+剩餘重量;原來重量-剩餘重量=運出重量)
教師應指出:(1)這兩種相等關係的表達形式與“原來重量-運出重量=剩餘重量”,雖形式上不同,但實質是一樣的,可以任意選擇其中的一個相等關係來列方程
(2)例2的解方程過程較為簡捷,同學應注意模仿.
依據例2的分析與解答過程,首先請同學們思考列一元一次方程解套用題的方法和步驟;然後,採取提問的方式,進行反饋;最後,根據學生總結的情況,教師總結如下:
(1)仔細審題,透徹理解題意.即弄清已知量、未知量及其相互關係;用字母(如x)表示題中的未知數
(2)根據題意找出相等關係.(這是關鍵一步)
(3)根據相等關係,正確列出方程.即所列的方程應滿足兩邊的量要相等;方程兩邊的代數式的單位要相同;題中條件應充分利用,不能漏也不能將一個條件重複利用等
(4)求出所列方程的解
(5)檢驗後明確地、完整地寫出答案.這裡要求的檢驗應是,檢驗所求出的解既能使方程成立,又能使套用題有意義.
二元一次方程
人教版7年級數學下冊第四章會學到,冀教版7年級數學下冊第九章會學到。在人教版九年級上英語講愛因斯坦時也會涉及
定義
二元一次方程定義:一個含有兩個未知數,並且未知數的指數都是1的整式方程,叫二元一次方程(linearequationoftwounknowns)。
二元一次方程組定義:由兩個二元一次方程組成的方程組,叫二元一次方程組(systemoflinearequationoftwounknowns)。
二元一次方程的解:使二元一次方程兩邊的值相等的兩個未知數的值,叫做二元一次方程的解。
二元一次方程組的解:二元一次方程組的兩個公共解,叫做二元一次方程組的解。
一般解法
消元:將方程組中的未知數個數由多化少,逐一解決。
消元的方法有兩種:
代入消元
例:解方程組x+y=5①6x+13y=89②
解:由①得x=5-y③把③帶入②,得6(5-y)+13y=89,解得y=59/7
把y=59/7帶入③,得x=5-59/7,即x=-24/7
∴x=-24/7,y=59/7
這種解法就是代入消元法。
加減消元
例:解方程組x+y=9①x-y=5②
解:①+②,得2x=14,即x=7
把x=7帶入①,得7+y=9,解得y=2
∴x=7,y=2
這種解法就是加減消元法。
二元一次方程組的解有三種情況:
1.有一組解
如方程組x+y=5①6x+13y=89②的解為x=-24/7,y=59/7。
2.有無數組解
如方程組x+y=6①2x+2y=12②,因為這兩個方程實際上是一個方程(亦稱作“方程有兩個相等的實數根”),所以此類方程組有無數組解。
3.無解
如方程組x+y=4①2x+2y=10②,因為方程②化簡後為x+y=5,這與方程①相矛盾,所以此類方程組無解。
一元二次方程
含有一個未知數,並且未知數的最高次數是2的整式方程,這樣的方程叫做一元二次方程(quadratic equation in one unknown)。
由一次方程到二次方程是個質的轉變,通常情況下,二次方程無論是在概念上還是解法上都比一次方程要複雜得多。
一般形式
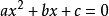 方程
方程(a≠0)
一般解法
一般解法有四種:
⒈公式法(直接開平方法)
⒉配方法
3.因式分解法
4.十字相乘法
十字相乘法能把某些二次三項式分解因式。這種方法的關鍵是把二次項係數a分解成兩個因數a,a的積a·a,把常數項c分解成兩個因數c,c的積c·c,並使ac+ac正好是一次項b,那么可以直接寫成結果:在運用這種方法分解因式時,要注意觀察,嘗試,並體會它實質是二項式乘法的逆過程。當首項係數不是1時,往往需要多次試驗,務必注意各項係數的符號。
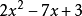 方程
方程例1 把 分解因式。
分析:先分解二次項係數,分別寫在十字交叉線的左上角和左下角,再分解常數項,分
別寫在十字交叉線的右上角和右下角,然後交叉相乘,求代數和,使其等於一次項係數.
分解二次項係數(只取正因數):
2=1×2=2×1;
分解常數項:
3=1×3=3×1=(-3)×(-1)=(-1)×(-3).
用畫十字交叉線方法表示下列四種情況:
1 1
╳
2 3
1×3+2×1
=5
1 3
╳
2 1
1×1+2×3
=7
1 -1
╳
2 -3
1×(-3)+2×(-1)
=-5
1 -3
╳
2 -1
1×(-1)+2×(-3)
=-7
經過觀察,第四種情況是正確的,這是因為交叉相乘後,兩項代數和恰等於一次項係數-7.
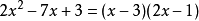 方程
方程解 .
一般地,對於二次三項式ax+bx+c(a≠0),如果二次項係數a可以分解成兩個因數之積,即a=aa,常數項c可以分解成兩個因數之積,即c=cc,把a,a,c,c,排列如下:
a c
╳
a c
ac+ac
按斜線交叉相乘,再相加,得到ac+ac,若它正好等於二次三項式ax+bx+c的一次項係數b,即ac+ac=b,那么二次三項式就可以分解為兩個因式ax+c與ax+c之積,即
ax+bx+c=(ax+c)(ax+c).
像這種藉助畫十字交叉線分解係數,從而幫助我們把二次三項式分解因式的方法,通常叫做十字相乘法。
例2 把 分解因式.
分析:按照例1的方法,分解二次項係數6及常數項-5,把它們分別排列,可有8種不同的排列方法,其中的一種
2 1
╳
3 -5
2×(-5)+3×1=-7
是正確的,因此原多項式可以用十字相乘法分解因式。
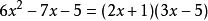 方程
方程解
指出:通過例1和例2可以看到,運用十字相乘法把一個二次項係數不是1的二次三項式因式分解,往往要經過多次觀察,才能確定是否可以用十字相乘法分解因式.
對於二次項係數是1的二次三項式,也可以用十字相乘法分解因式,這時只需考慮如何把常數項分解因數。例如把 分解因式,十字相乘法是
1 -3
╳
1 5
1×5+1×(-3)=2
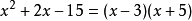 方程
方程所以 .
例3 把 分解因式。
分析:這個多項式可以看作是關於x的二次三項式,把-8y^2看作常數項,在分解二次項及常數項係數時,只需分解5與-8,用十字交叉線分解後,經過觀察,選取合適的一組,即
1 2
╳
5 -4
1×(-4)+5×2=6
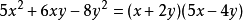 方程
方程解 .
指出:原式分解為兩個關於x,y的一次式。
例4 把(x-y)(2x-2y-3)-2分解因式.
分析:這個多項式是兩個因式之積與另一個因數之差的形式,只有先進行多項式的乘法運算,把變形後的多項式再因式分解。
問:兩上乘積的因式是什麼特點,用什麼方法進行多項式的乘法運算最簡便?
答:第二個因式中的前兩項如果提出公因式2,就變為2(x-y),它是第一個因式的二倍,然後把(x-y)看作一個整體進行乘法運算,可把原多項式變形為關於(x-y)的二次三項式,就可以用十字相乘法分解因式了.
解 (x-y)(2x-2y-3)-2
=(x-y)[2(x-y)-3]-2
=2(x-y)-3(x-y)-2
=[(x-y)-2][2(x-y)+1]
=(x-y-2)(2x-2y+1).
1 -2
╳
2 1
1×1+2×(-2)=-3
指出:把(x-y)看作一個整體進行因式分解,這又是運用了數學中的“整體”思想方法。
例5 x+2x-15
分析:常數項(-15)<0,可分解成異號兩數的積,可分解為(-1)(15),或(1)(-15)或(3)
(-5)或(-3)(5),其中只有(-3)(5)中-3和5的和為2。
=(x-3)(x+5)
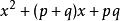 方程
方程總結:① 型的式子的因式分解
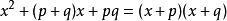 方程
方程這類二次三項式的特點是:二次項的係數是1;常數項是兩個數的積;一次項係數是常數項的兩個因數的和.因此,可以直接將某些二次項的係數是1的二次三項式因式分解:
②kx+mx+n型的式子的因式分解
如果能夠分解成k=ac,n=bd,且有ad+bc=m 時,那么
kx+mx+n=(ax+b)(cx+d)
a b
╳
c d
1.直接開平方法:
直接開平方法就是用直接開平方求解一元二次方程的方法。用直接開平方法解形如 的
方程,其解為 .
例1.解方程(1)(3x+1)=7 (2)9x-24x+16=11
分析:(1)此方程顯然用直接開平方法好做,(2)方程左邊是完全平方式(3x-4),右邊=11>0,所以
此方程也可用直接開平方法解。
(1)解:(3x+1)=7×
∴(3x+1)=5
∴3x+1=±(注意不要丟解)
∴x=
∴原方程的解為x=,x=
(2)解: 9x-24x+16=11
∴(3x-4)=11
∴3x-4=±
∴x=
∴原方程的解為x=,x=
2.配方法:用配方法解方程ax+bx+c=0 (a≠0)
先將常數c移到方程右邊:ax+bx=-c
將二次項係數化為1:x+x=-
方程兩邊分別加上一次項係數的一半的平方:x+x+( )=- +( )
方程左邊成為一個完全平方式:(x+ )=
當b-4ac≥0時,x+ =±
∴x=(這就是求根公式)
例2.用配方法解方程 3x-4x-2=0
解:將常數項移到方程右邊 3x-4x=2
將二次項係數化為1:x-x=
方程兩邊都加上一次項係數一半的平方:x-x+( )= +( )
配方:(x-)=
直接開平方得:x-=±
∴x=
∴原方程的解為x=,x= .
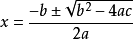 方程
方程3.公式法:把一元二次方程化成一般形式,然後計算判別式△=b-4ac的值,當b-4ac<0時,無解;方程當b-4ac≥0時,把各項係數a, b, c的值代入求根公式 就可得到方程的根。
例3.用公式法解方程2x-8x=-5
解:將方程化為一般形式:2x-8x+5=0
∴a=2, b=-8, c=5
b-4ac=(-8)-4×2×5=64-40=24>0
∴x= = =
∴原方程的解為x=,x= .
4.因式分解法:把方程變形為一邊是零,把另一邊的二次三項式分解成兩個一次因式的積的形式,讓
兩個一次因式分別等於零,得到兩個一元一次方程,解這兩個一元一次方程所得到的根,就是原方程的兩個根。這種解一元二次方程的方法叫做因式分解法。
例4.用因式分解法解下列方程:
(1) (x+3)(x-6)=-8 (2) 2x+3x=0
(3) 6x+5x-50=0 (選學) (4)x-2( + )x+4=0 (選學)
(1)解:(x+3)(x-6)=-8 化簡整理得
x-3x-10=0 (方程左邊為二次三項式,右邊為零)
(x-5)(x+2)=0 (方程左邊分解因式)
∴x-5=0或x+2=0 (轉化成兩個一元一次方程)
∴x=5,x=-2是原方程的解。
(2)解:2x+3x=0
x(2x+3)=0 (用提公因式法將方程左邊分解因式)
∴x=0或2x+3=0 (轉化成兩個一元一次方程)
∴x=0,x=-是原方程的解。
注意:有些同學做這種題目時容易丟掉x=0這個解,應記住一元二次方程有兩個解。
(3)解:6x+5x-50=0
(2x-5)(3x+10)=0 (十字相乘分解因式時要特別注意符號不要出錯)
∴2x-5=0或3x+10=0
∴x1=, x2=- 是原方程的解。
(4)解:x-2(+ )x+4 =0 (∵4 可分解為2 ·2 ,∴此題可用因式分解法)
(x-2)(x-2 )=0
∴x=2 ,x=2是原方程的解。
二元二次方程:含有兩個未知數且未知數的最高次數為2的整式方程。
三元一次方程
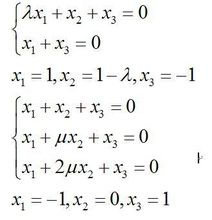 方程
方程與二元一次方程類似,三個結合在一起的共含有三個未知數的一次方程。
解法
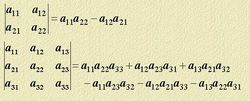 方程
方程與二元一次方程類似,可以利用消元法逐步消元。
典型題析
某地區為了鼓勵節約用水,對自來水的收費標準作如下規定:每月每戶用水不超過10噸按0.9元/噸收費;超過10噸而不超過20噸按1.6元/噸收費;超過20噸的部分按2.4元/噸收費。某月甲用戶比乙用戶多繳水費16元,乙用戶比丙用戶多繳水費7.5元。已知丙用戶用水不到10噸,乙用戶用水超過10噸但不到20噸.問:甲。乙.丙三用戶該月各繳水費多少元(按整噸計算收費)?
解:設甲用水x噸,乙用水y噸,丙用水z噸
顯然,甲用戶用水超過了20噸
故甲繳費:0.9*10+1.6*10+2.4*(x-20)=2.4x-23
乙繳費:0.9*10+1.6*(y-10)=1.6y-9
丙繳費:0.9z
2.4x-23=1.6y-7+16
1.6y-7=0.9z+7.5
化簡得
3x-2y=40……(1)
16y-9z=145……(2)
由(1)得x=(2y+40)/3
所以設y=1+3k,3<7
當k=4,y=13,x=22,代入(2)求得z=7
當k=5,y=16,代入(2),z沒整數解
當k=6,y=19,代入(2),z沒整數解
所以甲用水22噸,乙用水13噸,丙用水7噸
甲用水29.8元,乙用水13.8元,丙用水6.3元
多元一次方程
消元法
設方程組①:
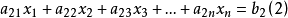 方程
方程……………………
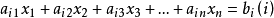 方程
方程……………………
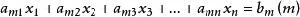 方程
方程把方程(1)×(-i/a)加到(i)上,再把方程(2)×(-i/a)加到(i)上,以此類推。(i∈N且i∈[1,m])最後,方程組變為:②
b x+b x+b x+…+b x=c
b x+b x+…+b x=c
………………
b x=c
0=c+1
0=0
0=0
………… (bii≠0,i=1,2,…r)
最後的許多0=0可以捨去,不影響方程的解。可以分三種情況:
(1)c+1 ≠0
此時,滿足前r各方程的任意一個解,都不能滿足0=c+1這個方程,所以②無解,所以①也無解
當c+1=0時,又分兩種情況:
(2)r=n
因為b≠0,所以從最後一個方程可解出x。然後代入第r-1個方程,解出x-1。如此類推,可得出方程組②的唯一解,就是方程組①的唯一解。
(3)r
可把方程組該成他的同解方程組③:
b x+b x+b x+…+b x=c-b,r+1 x+1-…-b x
b x+b x+…+b x=c-b,r+1 x+1-…-b x
………………
b x=c-b,r+1 x+1-…-b x
設等號後面的數是已知數,按照(2)的方法來解,可解得:
x=d x+1+d x+2+…+d,n-r x
x=d x+1+d x+2+…+d,n-r x
………………
x=d x+1+d x+2+…+d,n-r x
令自由未知量xr+i=ki(i∈N且i∈[1,n-r])可得方程組的全部解:
x=d k+d k+…+ d,n-r k
x=d k+d k+…+d,n-r k
………………
x=d k+d k+…+d,n-r k
x+1=k
x+2=k
…………
x=k
其他解法
克萊姆法則
(此法只適用於m=n且D≠0的方程組)
設係數行列式D=∣a ij∣,Di是D把i列換成結果的行列式
那么xi=Di/D(i∈N且i∈[1,n])
矩陣和向量解法
矩陣解法即把方程組①的增廣矩陣進行初等行變化。
向量解法即把方程組①改寫成Ax=b的形式。
先求出方程組的特解η,然後求其對應導出組Ax=0的解ξ,ξ,…,ξ。
方程組的解為:η+cξ+cξ+…+cξ。
直線方程
(1)一般式: Ax+By+C=0 (其中A、B不同時為0) 適用於所有直線
 方程
方程直線lAx+By+C=0
直線lAx+By+C=0
兩直線平行時:A1/A2=B1/B2≠C1/C2
兩直線垂直時:A1A2+B1B2=0
兩直線重合時:A1/A2=B1/B2=C1/C2
兩直線相交時:A1/A2≠B1/B2
(2)點斜式: 知道直線上一點(x,y),並且直線的斜率k存在,則直線可表示為 y-y=k(x-x)。當k不存在時,直線可表示為 x=x
(3)截距式: 若直線與x軸交於(a,0),與y軸交於(0,b),則直線可表示為:x/a+y/b=1。所以不適用於和任意坐標軸垂直的直線和過原點的直線 。
(4)斜截式: y=kx+b (k≠0)
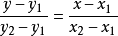 方程
方程(5)兩點式:若直線過任意兩點(x,y)、(x,y),且 x≠x,y≠y,則直線可以表示為
(6)法線式: x·cosα+ysinα-p=0
附註
一般地,n元一次方程就是含有n個未知數,且含未知數項次數是1的方程,一次項係數規定不等於0;
n元一次方程組就是幾個n元一次方程組成的方程組(一元一次方程除外);
一元a次方程就是含有一個未知數,且含未知數項最高次數是a的方程(一元一次方程除外);
一元a次方程組就是幾個一元a次方程組成的方程組(一元一次方程除外);
n元a次方程就是含有n個未知數,且含未知數項最高次數是a的方程(一元一次方程除外);
n元a次方程組就是幾個n元a次方程組成的方程組(一元一次方程除外);
方程(組)中,未知數個數大於方程個數的方程(組)叫做不定方程(組),此類方程(組)一般有無數個解。
雞兔同籠問題
解法公式
解法1:(兔的腳數×總只數-總腳數)÷(兔的腳數-雞的腳數)=雞的只數
總只數-雞的只數=兔的只數
解法2:(總腳數-雞的腳數×總只數)÷(兔的腳數-雞的腳數)=兔的只數
總只數-兔的只數=雞的只數
解法3:總腳數÷2—總頭數=兔的只數
總只數—兔的只數=雞的只數
解法4(方程):X=總腳數÷2—總頭數(X=兔的只數)
總只數—兔的只數=雞的只數
解法5(方程):X=(總腳數-雞的腳數×總只數)÷(兔的腳數-雞的腳數)(X=兔的只數)
總只數—兔的只數=雞的只數
解法6(方程):X=(兔的腳數×總只數-總腳數)÷(兔的腳數-雞的腳數)(X=雞的只數)
總只數-雞的只數=兔的只數
方程解法
若用方程解雞兔同籠問題,公式為:雞腳+兔腳=總腳數。
雞為x
例籠中共有30隻雞和兔,數一數足數正好是100隻。問雞和兔各有多少只?
解:設雞為x只,則兔為(30-x)只。
2x+(30-x)×4=100
解:2x+120-4x=100
120-2x=100
2x=20
x=10
30-10=20(只)
答:雞和兔各有10隻,20隻。
兔為x
例籠中共有雞兔100隻,雞兔足數共248隻。問雞兔各有多少只?
解:設兔為x只,則雞為(100-x)只。
4x+(100-x)×2=248
解:4x+200-2x=248
2x+200=248
2x=48
x=24
100-24=76(只)
答:雞兔各有76隻,24隻。
並不是所有方程都能列
之所以提到這點。是因為在解套用題的時候,有時也會列出這樣的方程。
例子:媽媽今年30歲,小明比媽媽小25歲。求小明多少歲?
解:設小明x歲。
這道方程有3種列法。
(1)等量關係1:小明+年齡差=媽媽
x+25=30
(2)等量關係2:媽媽-小明=年齡差。
30-x=25
誤區:(3)等量關係3:媽媽-年齡差=小明
30-25=x
“30-25=x這個等式擁有未知數,它是方程。但是,要是用這種方法解題,
就近似在一、二年級的算術方法了,30-25,我們口算都能得出結論,是5,那么何必要大廢周章去設x呢?還要活受罪寫解設。
方程分類
方程分類 形如… 未知數個數 未知數最高指數冪 未知數係數 解/根
實數方程
整式方程
(有理式)
一元 一元一次方程 ax+b=0(a≠0) 1 1 2 x
一元二次方程 ax2+bx+c=0(a≠0) 1 2 3 x1,x2
一元三次方程 ax3+bx2+cx+d=0(a≠0) 1 3 4 x1,x2,x3
一元四次方程 ax4+bx3+cx2+dx+e=0(a≠0) 1 4 5 x1,x2,x3,x4
二元 二元一次方程(*組) ax+by+c=0(a、b≠o) 2 1 3 1組
二元二次方程(*組) ax2+bxy+cy2+dx+ey+f=0。(a、b、c、d、e、f都是常數,且a、b、c中至少有一個不是零;當b為零時,a與d以及c與e分別不全為零 2 2 6 2組
分式方程 特殊 分母中有未知數(非常數) 1個以上 -1 2個以上
2個以上(偶數個)
有可能有增根出現
虛數/無理方程
無解方程
特殊類別 1 不定 不定 不存在
矛盾方程組 *特殊類別 不定 不定 不定 增根
概念 不定方程-定方程 *特殊類別 2或其他 不定 2或其他 多組
高次方程、三元一次方程、多元一次方程