異面直線所成角

（註：當所成角為90°時，兩直線垂直。 2反證法：假設兩條直線不異面，則不是平行就是相交。 兩條異面直線的公垂線段的長度，叫兩條異面直線的距離。

定義

過空間任意一點引兩條直線分別平行於兩條異面直線

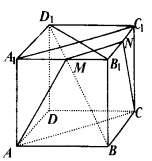如果BB1與B1D1異面直線成直角

，它們所成的銳角（或直角）就是異面直線所成的角。角的範圍是θ∈（0°,90°]
（註：當所成角為90°時，兩直線垂直。）

異面直線所成角的求法

求兩條異面直線所成角的大小一般方法是通過平行移動直線，把異面問題轉化為共面問題來解決的。

判定或證明兩條直線為異面直線的方法

1.根據異面直線的定義

：把不在任何一個平面內的兩條直線叫做異面直線。

2.異面直線的判定方法。

1平移法

：將兩條直線平移到同一平面，若相交，且在未平移之前不相交稱之為異面直線。

2反證法

：假設兩條直線不異面，則不是平行就是相交。假設一：相交——若相交則兩條直線有公共交點且共面，若不相交則證明假設二，假設二：平行——若平行則兩直線平移無交點，若不成立，則假設二不成立，則假設不成立，所以兩直線異面。或假設兩直線共面，並證明不成立。

3直接證明：證明兩條直線不平行且不相交4.坐標法：

選取空間坐標原點，建立空間坐標系並將兩條直線上任意兩點的坐標讀出，並計算出兩直線的向量，比較其是否為平行向量若是則兩直線不異面。並用具體條件證明其不相交即可證明兩直線為異面直線

異面直線所成角定義

異面直線

1.直線a，b是異面直線，經過空間一點O，分別引直線A//a,B//b,相交直線A，B所成的銳角（或直角）叫做異面直線a,b所成的角。
2. 異面直線所成角的計算。
（1）平移其中一條或兩條使其相交。
（2）連線端點，使角在一個三角形中。
（3）計算三條邊長，用餘弦定理計算餘弦值。
（4）若餘弦值為負，則取其相反數。

公垂線

與兩條異面直線均垂直、相交的直線叫兩條異面直線的公垂線，兩條異面直線的公垂線有且只有一條。

兩條直線垂直

（1）相交垂直 （2）異面垂直
兩條異面直線的公垂線段的長度，叫兩條異面直線的距離。