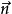有關定理
定理一:任意兩條異面直線有且只有一條公垂線。
定理二:兩條異面直線的公垂線段長(異面直線的距離)是分別連結兩條異面直線上兩點的線段中最短的一條。
常用計算方法
(1)找出(或作出)公垂線,計算公垂線段的長度。
(2)轉化為求線面間的距離。
過其中一條直線b上的任一點作另一條直線a的平行線c,b和c所決定的平面α與a之間的距離就是異面直線的距離。
(3)轉化為求平行平面間的距離。
過兩條異面直線作兩個互相平行的平面,這兩個平面間的距離就是異面直線的距離。
(4)向量方法:先求兩異面直線的公共法向量,再求兩異面直線上任意兩點的連結線段在公共法向量上的射影長。
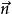 異面直線的距離
異面直線的距離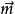 異面直線的距離
異面直線的距離 異面直線的距離
異面直線的距離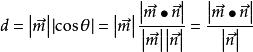 異面直線的距離
異面直線的距離公共法向量可以運用向量積找到,設任意兩點所連成的向量為,它們的夾角為,則異面直線的距離
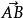 異面直線的距離
異面直線的距離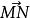 異面直線的距離
異面直線的距離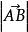 異面直線的距離
異面直線的距離該公式可以這樣理解:設異面直線AM和BN,其中AB是公垂線,M、N是兩條直線上任意的兩點。明顯地,MA⊥AB,NB⊥AB,根據射影的定義可知,是的射影,而就是異面直線的距離。
(5)若兩條異面直線在某一平面上的射影互相平行(或為一點和一直線),則可以求平行線的距離(或點到直線的距離),該距離就是異面直線的距離。
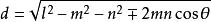 異面直線的距離
異面直線的距離(6)幾何公式法:設有兩條異面直線a、b,a、b的公垂線AB長為d。在a上找另一點C,b上找另一點D,AC=m,BD=n,CD=l,異面直線AC和BD所成角為θ。則 。注意正負號的使用,當二面角C-AB-D為θ時取+,為π-θ時取-。
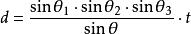 異面直線的距離
異面直線的距離第二公式:設異面直線a、b分別位於二面角α-l-β的半平面上,a與l交點為M,b與l交點為N,且MN=t。a與l的夾角為θ1,b與l夾角為θ2,二面角大小為θ3,a、b所成角為θ,則a、b之間距離為
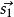 異面直線的距離
異面直線的距離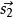 異面直線的距離
異面直線的距離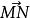 異面直線的距離
異面直線的距離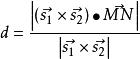 異面直線的距離
異面直線的距離(7)向量公式法:設兩條異面直線的方向向量為和,是兩條直線上任意一點的連線的方向向量,則異面直線的距離
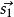 異面直線的距離
異面直線的距離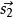 異面直線的距離
異面直線的距離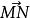 異面直線的距離
異面直線的距離該公式具有明顯的幾何意義。分子是、和所構成的平行六面體的體積,分母是該平行六面體的底面積,異面直線的距離就是平行六面體的高。根據體積公式得h=V/S。
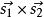 異面直線的距離
異面直線的距離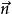 異面直線的距離
異面直線的距離參考(4)的求法,我們可以發現恰好就是兩條異面直線的公共法向量,所以這兩條公式從本質上來說是一樣的,只不過解讀的角度不同而已。