基本介紹
狄拉克（Dirac）符號（也叫“bra-ket 符號”）於1939年被狄拉克提出，他將“括弧（bracket）”這個單詞一分為二，分別代表這個符號的左右兩部分，左邊是“bra”，即為左矢；右邊是“ket”，即為右矢。
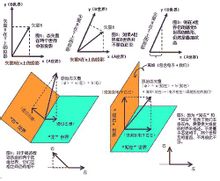狄拉克符號把希爾伯特空間一分為二，互為對偶的空間，就是狄拉克符號的優點。用右矢|α>表示態矢，左矢<α|表示其共厄矢量，><α|β>是內積，<α|α>大於等於0，稱為模方。|β><α|是外積。>
注意的是：幾種表示的意義：|α> 右矢，<α| 左矢，A表示算符，A|α>表示一個右矢，<α|A表示一個左矢，而且，A總是從左方作用於右矢，從右方作用於左矢的。 ><α|A|β>是一個複數，可以看成（<α|A|）|β>即一個左矢與一個右矢的內積；或者<α|（A|β>），即一個右矢與一個左矢的內積。
狄拉克符號在量子力學理論表述中 有兩個優點：1.可以毋需採用具體表象（即可以脫離某一具體的表象）來討論問題。2.運算簡捷，特別是對於表象變換
矩陣表示
右矢與左矢可分別用N×1階和1×N階矩陣表示為：
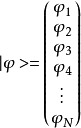狄拉克符號
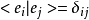狄拉克符號不同的兩個態矢量的內積則由一個括弧來表示：<ψ|φ>，當狄拉克符號作用於兩個基矢時，所得值為：
（δ為克羅內克函式）
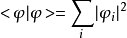狄拉克符號相同的態矢量內積為：
性質
因為每個右矢是一複數希爾伯特空間中的一個矢量，而每個右矢-左矢關係是內積，而直接地可以得到如下的操作方式：
（1）給定任何左矢<Φ|、右矢|Ψ>以及|Ψ>複數c及c，則既然左矢是線性泛函，根據線性泛函的加法與標量乘法的定義有：
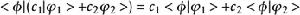狄拉克符號（2）給定任何右矢|Ψ>、左矢<Φ|以及><Φ|，還有複數c及c，則既然右矢是線性泛函：>
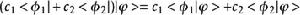狄拉克符號（3）給定任何右矢|Ψ>以及|Ψ>，還有複數c及c，根據內積的性質（其中c*代表c的複數共軛），則有：
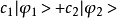狄拉克符號和
對偶。
（4）給定任何左矢<Φ|及右矢|Ψ>，內積的一個公理性質指出：
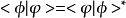狄拉克符號內積計算性質
1. 狄拉克符號和波函式的關係
<x|ψ>=ψ(x)
把x換成p也一樣，這裡|x>,|p>滿足關係
X|x>=x|x>，P|p>=p|p>
此時，X,P是坐標和動量算符，x,p都是具體的坐標動量值。
2最基本的不確定關係
<x|p>=aexp(ipx/h)
三維換成點乘，歸一化係數a=1/（2pih）^(s/2),s是維度）
注意：h是帶一橫的。
3一個力學量A在|ψ〉上的觀測值是<ψ|A|ψ>，A是一個厄米算符，A=A(+)
4<a|ABC...|b> 是一個經典數，在式子中可以作為（表示，但是不能表示高等數學）一個整體移動，其他情況下，你不能改變式子中各符號的順序。(<a|ABC...|b>)*=(<b|...C(+)B(+)A(+)|a>),(在當中是力學量算符的情況下，不用寫(+))
5.薛丁格表象：
|ψ（t）>=exp(-iHt)|ψ>或者說滿足薛丁格方程。
力學量A不隨時間演化。任意時刻對力學量A的觀測平均值為<ψ|exp(iHt)Aexp(-iHt)|ψ>
海森堡表象，態不變，力學量算符按照時間演化
A(t)=exp(iHt)Aexp(-iHt)
保證在任意時刻測量得到的力學量平均值與薛丁格表象下是一致的。直接對A(t)求導推出海森堡方程
力學量的指數表示exp(A)=1+A+A^2/2!+A^3/3!+....
驗證作用在力學量A的本徵態|a>上時，滿足exp(A)|a>=exp(a)|a>
影響
量子力學對矩陣計算有重要影響。狄拉克符號的創新套用在它能表示動態過程。
