簡介
全體調和函式的總體，是拉普拉斯方程
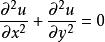狄利克雷問題的所有解的總體，這方程是最簡單的二階偏微分方程之一.類似於常微分方程情形，為了可以區分出一個確定的解而給出了附加的條件.完全一樣，為了要完全確定拉普拉斯方程的一個解，也需要一些附加的條件.對於拉普拉斯方程的這些條件，通常表述成稱之謂邊值條件的形狀，即，表述成所求解在區域的邊界上所應當滿足的一些給定關係式的形狀.這樣的邊值條件，可以由所給問題的解的那些物理條件本身，自然地得到。
這類條件中最簡單的那一種，歸結為在區域的邊界的每一點上給定所求的調和函式的值。由此，產生了所謂第一邊值問題，或者，狄利克雷問題：
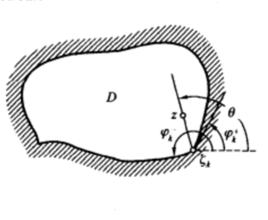
狄利克雷問題求出一個在區域D內調和並且在內連續的函式u(z)，使它在D的邊界上取已經給定的連續值u(ξ)。
舉例
例如，在某一區域內求熱場的溫度或靜電場的勢能，當在這區域的邊界上的溫度或勢能已經知道時，便可化為狄利克雷問題。
在套用中，邊界值u(ξ)是連續的這個條件，是限制過嚴了，所以需要考慮廣義狄利克雷問題：
設已經在區域D的邊界C上給出了一個函式u(ξ)，它出了在有限多個點ξ1，ξ2，…，ξn處有第一類間斷點外，是處處連續的。要求找出一個在區域D內的有界調和函式u(z)，使它在函式u(ξ)的所有連續點處都取值u(ξ)**。
橢圓型方程的狄利克雷問題
狄利克雷問題
狄利克雷問題
狄利克雷問題 狄利克雷問題 狄利克雷問題求二階橢圓型方程在區域邊界上的值為已知的解。設區域的邊界為。求在上連續、在內滿足給定的橢圓型方程、在上取給定的連續邊界值的解的問題，稱為橢圓型方程的狄利克雷問題。
狄利克雷問題特別地，對有界區域，如果邊界點都是正則點（參見“閘函式”），調和方程△u=0的狄利克雷問題的解存在且位移。
對於一般的強橢圓型方程
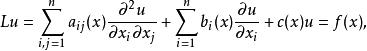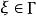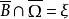狄利克雷問題 狄利克雷問題
狄利克雷問題
狄利克雷問題 狄利克雷問題 狄利克雷問題 狄利克雷問題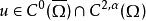
狄利克雷問題如果c(x)≤0，f 及 L 的係數有界並屬於C (Ω)。假設有界的每一邊界點上滿足外部球條件；即對每一點，存在一個球B=B(y)滿足。如果φ在上連續，那么狄利克雷問題：在中Lu=f，在上u=φ就有惟一解。
