熱帶幾何

熱帶幾何（Tropical geometry）是數學的一支，首先由巴西數學家兼計算機科學家 Imre Simon 於 1980 年代發展；“熱帶”一詞源於部分法國數學家對巴西的刻板印想。大略言之，熱帶幾何可謂是分片線性化的代數幾何。它在計數代數幾何中有重要的套用。

基本定義

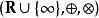熱帶幾何

定義 熱帶半環（又稱極小-加法代數，見下述定義）為 ，其運算為：

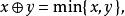熱帶幾何

熱帶幾何

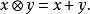熱帶幾何

此半環中的單項式不外就是線性映射；而多項式是對若干個線性映射取極小值，因此是個分片線性凹函式。稱之為 熱帶多項式。一個熱帶多項式 的非光滑點集合稱為 熱帶超曲面。可以證明：

1、熱帶超曲面即是滿足“零張力條件”的有理多面體復形。

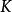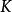熱帶幾何

熱帶幾何

2、設為皮瑟級數環，這是一個代數封閉的非阿基米德域。熱帶超曲面即上的變形體。

上述兩種刻劃提供了組合學與代數學之間的對應。給定一個合適的代數問題，我們可將之轉化為較易處理的組合問題以求解。

代數幾何中的情況

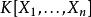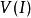熱帶幾何

熱帶幾何

熱帶幾何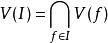

熱帶幾何

熱帶幾何

如代數幾何中的情形，熱帶超曲面的定義可以推廣到 熱帶簇：取中的理想，定義相應的熱帶簇為的變形體。可以證明，而且可取有限並集。

目前已有較深入研究的是平面上的熱帶幾何。許多代數幾何中的古典定理皆有相應的版本。