設{u‑}為一序列,u1u2. "un…或記為
稱為無窮乘積.
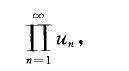
無窮乘積(infinite product)是把無窮序列的各項用乘號連結得到的表達式。
設{u‑}為一序列,u1u2. "un…或記為
稱為無窮乘積.
無窮乘積機率空間:數學術語
典範乘積(canonical product)是對應於非零序列的外爾斯特拉斯基本因式構成的無窮乘積 ,與其相關的定理有維爾斯特拉斯定理,阿達馬定理等。
基本介紹 相關分析數論中,歐拉乘積公式(Euler product formula)是指狄利克雷級數可表示為一指標為素數的無窮乘積。這一乘積以瑞士數學家萊昂哈德·歐拉的名...
簡介 定義 證明無窮級數是研究有次序的可數或者無窮個數函式的和的收斂性及和的數值的方法,理論以數項級數為基礎,數項級數有發散性和收斂性的區別。只有無窮級數收斂時有一個和...
概述 歷史 記號 性質 冪級數無窮小量是數學分析中的一個概念,在經典的微積分或數學分析中,無窮小量通常以函式、序列等形式出現。 無窮小量即以數0為極限的變數,無限接近於0。確切地說,...
定義 性質 無窮大 階的比較在數學上,以法國數學家奧古斯丁·路易·柯西命名的柯西乘積,是指兩組數列{\displaystyle a_n,b_n}的離散卷積。
級數 示例[編輯] 收斂和梅爾滕斯定理[編輯] 切薩羅定理[編輯]《形的殿堂》介紹幾何思想方法源頭,探討在現實生活中的套用,研究幾何學與人文教育的聯繫,了解幾何學現代發展。主要內容包括:幾何公理體系與中學初等幾何、幾何...
內容簡介 圖書目錄《無窮級數與連分數》比較系統地對無窮級數在數學中所起的技術工具作用與連分數解析理論構造閔可夫斯基(Minkowski)函式及將其開拓到複數域上作了介紹。
內容簡介 目錄《無窮分析引論(上)》是作為微積分預備教程,為彌補初等代數對於微積分的不足,為學生從有窮概念向無窮概念過渡而寫,讀者對象是準備攻讀和正在攻讀數學的學生、...
基本介紹 圖書目錄