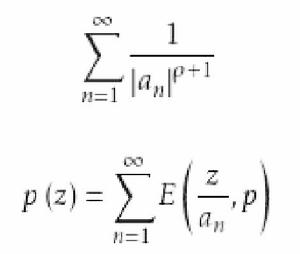基本介紹
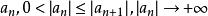 典範乘積
典範乘積 典範乘積
典範乘積典範乘積是對應於非零序列的外爾斯特拉斯基本因式構成的無窮乘積,設有序列,是使
 典範乘積
典範乘積收斂的最小非負整數,稱
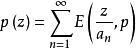 典範乘積
典範乘積 典範乘積
典範乘積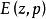 典範乘積
典範乘積為序列的典範乘積,這裡是外爾斯特拉斯基本因式 。
相關分析
 典範乘積
典範乘積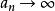 典範乘積
典範乘積定理1存在一個具有任意規定的零點的整函式,只要在零點為無窮多的情形下,,.除這些零點之外別無其他零點的任意整函式可以表示成如下形式:
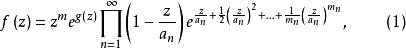 典範乘積
典範乘積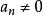 典範乘積
典範乘積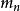 典範乘積
典範乘積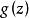 典範乘積
典範乘積其中,乘積是對所有的取的,為某些整數,為一個整函式 。
這一定理是由魏爾斯特拉斯提出的,它具有如下一條重要的推論:
推論 在整個平面上的任意亞純函式必是兩個整函式之商。
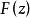 典範乘積
典範乘積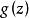 典範乘積
典範乘積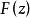 典範乘積
典範乘積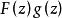 典範乘積
典範乘積 典範乘積
典範乘積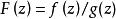 典範乘積
典範乘積這是因為,如果設在整個平面上是亞純的,則可求得一個整函式,以的極點作為該函式的零點,於是積是一個整函式,記為,即得,
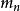 典範乘積
典範乘積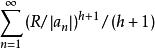 典範乘積
典範乘積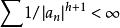 典範乘積
典範乘積在表示式(1)中,如果能選擇所有的互等,則該表示式就更為重要,上面的證明表明,只要級數對所有的R收斂,也就是說,只要,則無窮乘積
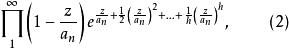 典範乘積
典範乘積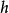 典範乘積
典範乘積 典範乘積
典範乘積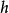 典範乘積
典範乘積收斂,而且表示一個整函式。設為使上述級數收斂的最小整數;於是表達式(2)就稱為與序列相關的 典範乘積,稱為典型乘積的 虧格。
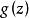 典範乘積
典範乘積 典範乘積
典範乘積 典範乘積
典範乘積在表示式(1)中,只要可能的話,我們總套用典範乘積,因此這一表示式是惟一確定的,如果在這一表示式中,化為一個多項式,則稱函式是有窮虧格的,而根據定義,的虧格就等於這個多項式的次數或典範乘積的虧格二者之中較大的數。
例如,虧格等於零的整函式具有下列形式
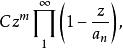 典範乘積
典範乘積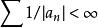 典範乘積
典範乘積且,虧格為1的整函式的典範表示或者為
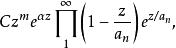 典範乘積
典範乘積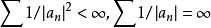 典範乘積
典範乘積其中,;或者為
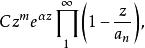 典範乘積
典範乘積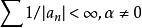 典範乘積
典範乘積其中。
 典範乘積
典範乘積定理2 阿達馬因子分解定理(Hadamard factorization theorem)是有窮級整函式的一種表示式。若函式是有窮級整函式,其級為ρ,則
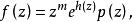 典範乘積
典範乘積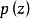 典範乘積
典範乘積 典範乘積
典範乘積 典範乘積
典範乘積 典範乘積
典範乘積其中是的零點的典範乘積,是次數不超過ρ的多項式,m是在原點的零點的級。