概述
在網路理論中,無尺度網路(或稱無標度網路)是帶有一類特性的複雜網路,其典型特徵是在網路中的大部分節點只和很少節點連線(節點的’度‘很小),而有極少的節點與非常多的節點連線(節點的’度‘非常高)。這種關鍵的節點(稱為“樞紐”或“集散節點”)的存在使得無尺度網路對意外故障有強大的承受能力,但面對協同性攻擊時則顯得脆弱。現實
中的許多網路都帶有無尺度的特性,例如網際網路、金融系統網路、社會人際網路等等。
源起
無尺度網路的概念是隨著對複雜網路的研究而出現的。“網路”其實就是數學中圖論研究的圖,由一群頂點以及它們之間所連的邊構成。在網路理論中則換一套說法,用“節點”代替“頂點”,用“連結”代替“邊”。複雜網路的概念,是用來描述由大量節點以及這些節點之間錯綜複雜的聯繫所構成的網路。這樣的網路會出現在簡單網路中沒有的特殊拓撲特性。自二十世紀60年代開始,對複雜網路的研究主要集中在隨機網路上。隨機網路,又稱隨機圖,是指通過隨機過程製造出的複雜網路。最典型的隨機網路是保羅·埃爾德什和阿爾弗雷德·倫伊提出的ER模型。ER模型是基於一種“自然”的構造方法:假設有n個節點,並假設每對節點之間相連的可能性都是常數0 < p < 1。這樣構造出的網路就是ER模型網路。科學家們最初使用這種模型來解釋現實生活中的網路。
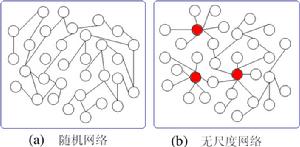
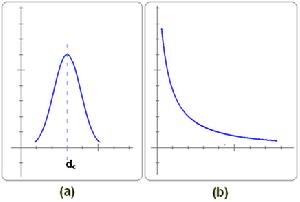
在一般的隨機網路(如ER模型)中,大部分的節點的度都集中在某個特殊值附近,成鐘形的泊松分布規律(見圖3)。偏離這個特定值的機率呈指數性下降,遠大於或遠小於這個值的可能都是微乎其微的,就如一座城市中成年居民的身高大致的分布一樣。然而在1998年,Albert-László Barabási、Réka Albert等人合作進行一項描繪全球資訊網的研究時,發現通過超連結與網頁、檔案所構成的全球資訊網網路並不是如一般的隨機網路一樣,有著均勻的度分布。他們發現,全球資訊網是由少數高連線性的頁面串聯起來的。絕大多數(超過80%)的網頁只有不超過4個超連結,但極少數頁面(不到總頁面數的萬分之一)卻擁有極多的連結,超過1000個,有一份檔案甚至與超過200萬個其他頁面相連。與居民身高的例子作類比的話,就是說大多數的節點都是“矮個子”,而卻又有極少數的身高百丈的“巨人”。Barabási等人將其稱為“無尺度”網路,所謂的無尺度,是從scale free翻譯而來,scale就是指節點度的大小,free 是指雖然網路中大部分節點的度不高,但極少數節點的度不受任何限制,可以變得十分巨大。
描述與定義
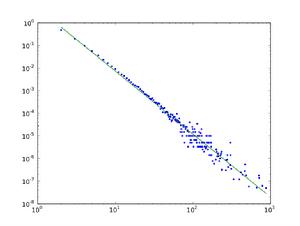
無尺度網路的特性,在於其度分布沒有一個特定的平均值指標,即大多數節點的度在此附近。在研究這個網路的度分布時,Barabási等人發現其遵守冪律分布(也稱為帕累托分布),也就是說,隨機抽取一個節點,它的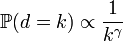
也就是說d = k 的機率正比於k 的某個冪次(一般是負的,記為 γ)。因此k越大,d = k 的機率就越低。然而這個機率隨k增大而下降的“速度”是比較緩慢的:在一般的隨機網路中,下降的速度是指數性的,而在無尺度網路中只是以多項式類的速度下降。
度-度相關性
僅僅是將度分布的冪律分布作為無尺度網路的定義有其不夠完善之處。由於冪律分布是方差可能無窮的高可變分布,對於度分布是同一個冪律分布的不同網路,其拓撲結構和特性可能存在巨大的差異。2005年,Lun Li和大衛·阿爾德森(David Alderson)等人在論文《邁向無標度圖的理論》(Towards a Theory of Scale Free Graphs)中提出了一種補充性的標度性測度。設G(D)為所有具有(依照冪律分布的)度分布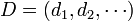
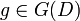
定義度-度相關數:
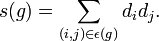
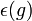
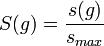
例子
不少現實中的網路結構都屬於無尺度網路,或者有無尺度的特性。以下是一些無尺度網路的例子:| 網路 | 節點 | 連線 |
|---|---|---|
| 電影演員網路 | 演員 | 出演同一部電影 |
| 全球資訊網 | 網頁 | 超連結 |
| 網際網路 | 路由器 | 物理連線 |
| 蛋白質相互作用網路 | 蛋白質 | 蛋白質之間的相互作用關係 |
| 金融網路 | 金融機構 | 借貸關係 |
| 美國飛機航班網路 | 機場 | 飛機航線 |
BA模型
Albert-László Barabási與Réka Albert在1999年的論文中提出了一個模型來解釋複雜網路的無尺度特性,稱為BA模型。這個模型基於兩個假設:增長模式:不少現實網路是不斷擴大不斷增長而來的,例如網際網路中新網頁的誕生,人際網路中新朋友的加入,新的論文的發表,航空網路中新機場的建造等等。
優先連線模式:新的節點在加入時會傾向於與有更多連線的節點相連,例如新網頁一般會有到知名的網路站點的連線,新加入社群的人會想與社群中的知名人士結識,新的論文傾向於引用已被廣泛引用的著名文獻,新機場會優先考慮建立與大機場之間的航線等等。
在這種假設下,BA模型的具體構造為:
增長:從一個較小的網路G0開始(這個網路有n0個節點,E0條邊),逐步加入新的節點,每次加入一個。
連線:假設原來的網路已經有n個節點。在某次新加入一個節點sn + 1時,從這個新節點向原有的n個節點連出m < n0個連結。
優先連線:連線方式為優先考慮高度數的節點。對於某個原有節點si(
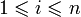
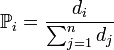
分析BA模型網路的漸近度分布(當節點數量很大時的度分布)主要有連續場理論、主方程法和速率方程法。這三種方法得到的漸近結果都是相同的。2001年,Béla Bollobás證明了在節點數量很大時,BA模型網路的度分布遵從γ = 3的冪律分布。之後,其它的無尺度網路模型也開始被提出。
其它無尺度模型
BA模型成功的為無尺度網路找到了一個簡單而合理的形成機制。然而,BA模型也有其自身的局限。例如,它只能描述γ = 3的無尺度網路,對於真實網路的一些非冪律特徵如指數截斷(exponential cutoff)、小變數飽和(saturation of small variables)等無法描述。因此,各種BA模型的推廣、變化版本開始出現。Bollobás在2001年提出了線性弦圖模型(LCD模型),允許節點自己與自己相連。而後又出現了只允許重複連線而不允許自連線的模型與不允許重複連線、自連線而是在選中的舊節點的鄰域隨機聯線的模型。適應度模型
在BA模型的製造過程中,人們發現,存在越久的節點具有越高的度數。然而,現實生活的網路中並非存在越久的元素就能有更多的聯繫。BA模型並沒有包括“後起之秀”的現象。於是,出現了基於BA模型的適應度模型。適應度模型主要是修正了優先連線的機制,對每個節點加上一個吸引因子μi,這樣新節點的相連機率改正為: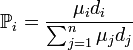
局域世界演化模型
另一種基於BA模型的推廣版本是局域世界演化模型。這個模型假設每個新節點在引入時並不能在全域進行優先連線。比如說一家新上市的公司可能只會與同地區或同國家的公司展開貿易聯繫,居民搬入新社區時只會與同一幢樓的人開始認識等等。局域世界演化模型將BA模型優先連線的機制改為:新加入的節點時,先選擇全部節點的一部分(隨機選取的M個節點)作為局域世界,然後再在局域世界中進行優先連線。模擬結果指出,當M從m變化到n0 + t時,產生的網路從服從指數分布逐漸過渡到服從冪律分布複製模型
在BA模型中,度分布實際上是和增長的時間t(或說增長次數)相關的,只是在t十分大時近似於度分布。複製模型是一個與增長時間無關的模型。複製模型的做法是每次隨機地“複製”一個原有的節點:即隨機選定一個節點i,再加入一個新節點,然後新節點按照i與其它舊節點連線的方式與舊節點相連,最後與i也相連分層模型
2001年,Barabási提出了第一個確定性的分層網路模型。這個模型是為了解釋生物學中γ≈2.2的代謝網路。分層模型的想法是從模體(motif)出發,通過自相似的層次疊加而得到複雜網路。這種思想類似於分數維圖形。Barabási的模型是: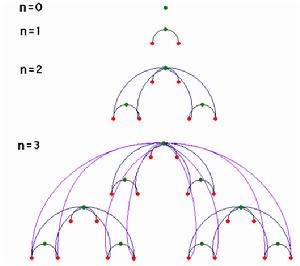
以一個一級模體作為根模體,再建立兩個一級模體,將它們的一級節點(一共4個)與根模體的根節點相連,這樣得到一個二級模體(右圖6中n=2的階段);
對二級模體重複前一步的操作(見右圖n=3的階段)。
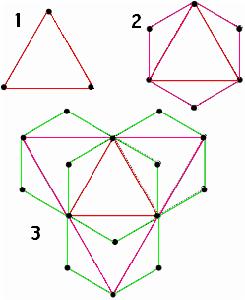
這樣形成的網路是無尺度網路,Barabási算出它的γ=log3/log2。後來有使用5節點4連結作為模體,得到γ = 1,而4節點3連結作為模體得到γ=1+log3/log2≈2.26,近似於代謝網路。需要注意的是此模型中不少度數是0機率的,所以需要使用補分布繞過。類似的確定性模型還有偽分形圖(pseudofractal scale-free network)以及阿波羅模型(Apollonian network)。
阿喀琉斯之踵
2000年7月27日,《自然》雜誌的封面文章標題是《網際網路的阿喀琉斯之踵》(Achilles' Heel of the Internet)。阿喀琉斯是古希臘神話中的英雄,他出生後,他的母親捏著他的腳踝將他浸泡在冥河中,從此他的身體刀槍不入,只有踵部沒被浸到,是為其致命弱點。因此如今“阿喀琉斯之踵”常被用來稱呼一個系統的致命缺陷。這篇文章中從網際網路的無尺度特性出發,探討它對意外故障的承受能力。假設在一個網路中移除一個節點,以及與其相關的連線,那么原網路中的其他點也可能受到影響:原本相連的兩個節點可能不再相連;即使相連,從其中一處到另一處可能需要經過更多的路途。總的來說,網路的連通性降低了。文章比較了ER隨機網路模型與BA模型在移除少量節點時對網路連通性的影響。這個影響主要使用最大連通子圖的大小S與平均路徑長度l來衡量。在執行“隨機攻擊策略”,也就是在網路中隨機地去除一些節點時,無尺度網路的S比隨機網路下降慢得多,l的增長也緩慢得多。但是在執行“蓄意攻擊策略”,也就是選擇移除連線度最高的節點時,則會得到相反的結果。受到隨機攻擊的隨機圖會分裂成幾個較小的子圖,而無尺度網路則有很大機率保持連通;然而面對蓄意攻擊(或稱協同攻擊)時,只需要移除5-10%的高於5度的節點,就能徹底癱瘓無尺度網路。
流行病臨界值
流行病或網路病毒在複雜網路中的傳播也是複雜網路研究的方向之一。在均勻網路如ER模型隨機網路或小世界網路中,如果考慮易感(S)→感染(I)→易感(S)的SIS模型,那么存在一個與網路特性相關的臨界值,當有效傳播率高於這個臨界值的時候,傳染病會在網路中傳播並穩定在某個恆定密度上(激活相態)。而當有效傳播率低於這個臨界值時,傳染病會很快逐漸消亡(吸收相態)。對於無尺度網路,由於度分布不均勻,臨界值比較小。對於BA模型,臨界值為0。也就是說,只要有效傳播率大於0,病毒就能有效傳播並達到穩定。而對於有限規模的無標度網路,臨界值大於0,但會在均勻網路的十分之一左右。因此,無標度網路對於病毒傳播的抵抗性較均勻網路脆弱得多。由於無尺度網路應對流行病感染的脆弱性,人們提出不同的免疫策略來彌補。主要研究的免疫策略有三種:隨機免疫、選擇免疫與熟人免疫。

