簡介
Heine定理
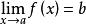 海涅定理
海涅定理 海涅定理
海涅定理 海涅定理
海涅定理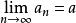 海涅定理
海涅定理 海涅定理
海涅定理 海涅定理
海涅定理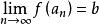 海涅定理
海涅定理存在的充要條件是:對屬於函式定義域的任意數列{},且,不等於,有.
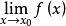 海涅定理
海涅定理 海涅定理
海涅定理 海涅定理
海涅定理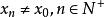 海涅定理
海涅定理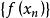 海涅定理
海涅定理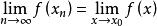 海涅定理
海涅定理海涅定理表明了函式極限與數列極限的關係。如果極限存在,為函式的定義域內任一收斂於x0的數列,且滿足:,那么相應的函式值數列必收斂,且.
作用
海涅定理是溝通函式極限和數列極限之間的橋樑。根據海涅定理,求函式極限則可化為求數列極限,同樣求數列極限也可轉化為求函式極限。因此,函式極限的所有性 質都可用數列極限的有關性質來加以證明。根據海涅定理的充分必要條件還可以判斷函式極限是否存在。所以在求數列或函式極限時,海涅定理起著重要的作用。 海涅定理是德國數學家海涅(Heine)給出的,套用海涅定理人們可把函式極限問題轉化(歸結)成數列問題,因而人們又稱它為歸結原則。
 海涅定理
海涅定理 海涅定理
海涅定理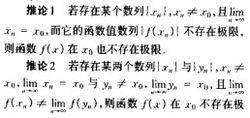 海涅定理
海涅定理 海涅定理
海涅定理雖然數列極限與函式極限是分別獨立定義的,但是兩者是有聯繫的。海涅定理深刻地揭示了變數變化的整體與部分、連續與離散之間的關係,從而給數列極限與函式極限之間架起了一座可以互相溝通的橋樑。它指出函式極限可化為數列極限,反之亦然。在極限論中海涅定理處於重要地位。有了海涅定理之後,有關函式極限的定理都可藉助已知相應的數列極限的定理予以證明。

