簡介
流形上微分運算元理論是流形上的分析的一個分支，它研究流形上橢圓微分運算元及擬微分運算元的阿蒂亞-辛格指標定理及其套用。
線性微分運算元
設M是緊可定向流形，E，F是M上的C復向量叢，線性映射P:C(E)→C(F)，其中C(E)與C(F)分別是E與F的C截面構成的復向量空間，若在局部坐標下P表示為向量微分運算元，則稱P為M上的線性微分運算元。類似地可定義M上的擬微分運算元。
橢圓運算元
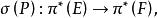流形上微分運算元理論對於這兩種運算元，可以定義叢同態 σ(P)是運算元P的象徵。若象徵是同構的話，微分運算元（或擬微分運算元）P就是橢圓運算元。
阿蒂亞-辛格指標
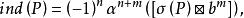流形上微分運算元理論對於橢圓運算元，阿蒂亞-辛格指標定理指出：橢圓運算元的指標 其中α是博特同構的疊代，b是貝蒂類，⊠是外積。
這個定理有三種證明方法：配邊證明、嵌入證明和熱方程證明。
套用
阿蒂亞-辛格定理有極廣泛的套用，能包容高斯-波涅公式、希策布魯赫符號差定理、黎曼-羅赫-希策布魯赫定理；推出萊夫謝茨公式及更廣泛的阿蒂亞-博特-萊夫謝茨數公式；能套用於有邊界的緊流形的橢圓型邊值問題，還可套用於規範場理論等。
發展
指標定理是阿蒂亞(Atiyah,M.F.)與辛格(Singer,I.M.)於1963年的一篇合作論文中首先發表的，繼而於1968年阿蒂亞和辛格又給出了指標定理的上同調形式。
阿蒂亞-辛格指標定理是分析學與拓撲學結合的範例。
