介紹
波格方程(Burgers equation)孤立子理論的重要方程之一一種帶有非線性項的擴散方程.其形式為
 波格方程
波格方程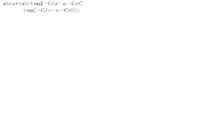 波格方程
波格方程於是波格方程的初值問題可精確求解.孤立子波可由試解}(x,t>=}(二一ct)求得.Burger方程的精確可解性誘導人們以此方程作為例子進行兩孤立子波之間相互作用的研究.從(4)式的解,能夠得到如下形式的兩個孤立子波:
其中a,CCz,二:及x:為適當的常數.
格方程(Burgers equation)孤立子理論的重要方程之一一種帶有非線性項的擴散方程.其形式為於是波格方程的初值問題可精確求解.孤立子波可由試解}(x,t>=}(二一ct)求得.Burger方程的精確可解性誘導人們以此方程作為例子進行兩孤立子波之間相互作用的研究.從(4)式的解,能夠得到如下形式的兩個孤立子波:
介紹
波格方程(Burgers equation)孤立子理論的重要方程之一一種帶有非線性項的擴散方程.其形式為
 波格方程
波格方程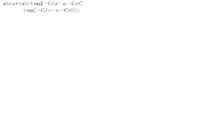 波格方程
波格方程於是波格方程的初值問題可精確求解.孤立子波可由試解}(x,t>=}(二一ct)求得.Burger方程的精確可解性誘導人們以此方程作為例子進行兩孤立子波之間相互作用的研究.從(4)式的解,能夠得到如下形式的兩個孤立子波:
其中a,CCz,二:及x:為適當的常數.
非線性方程,就是因變數與自變數之間的關係不是線性的關係,這類方程很多,例如平方關係、對數關係、指數關係、三角函式關係等等。求解此類方程往往很難得到精確解...
定義 分類 非線性代數方程 非線性微分方程 發展史在物理學裡,哈密頓-雅可比方程 (Hamilton-Jacobi equation,HJE) 是經典力學的一種表述。哈密頓-雅可比方程、牛頓力學、拉格朗...
簡介 數學表述 各種力學表述的比較 詳解 分離變數法格波,原子熱振動的一種描述。從整體上看,處於格點上的原子的熱振動可描述成類似於機械波傳播的結果,這種波稱為格波。
曾經有一個時期認為狄喇克方程是惟一正確的相對論量子力學方程。 以上所涉及的相對論量子力學方程僅限於描述一個粒子。
單粒子與多粒子體系的相對論量子力學方程 正文 配圖 相關連線在經典電動力學中,將描述電磁波的勢所滿足的一個微分方程組稱作達朗貝爾方程(英文:d'Alembert equation)。達朗貝爾方程是一個非齊次的波動方程。
簡介 形式 波動方程萊布尼茨方程,即常微分方程y'=x^2+y^2.語言表述為"求這樣一個函式,它的導數等於自變數與因變數的平方和".
介紹 發展克萊因-戈爾登方程(Klein-Gordon equation)是相對論量子力學和量子場論中的最基本方程,它是薛丁格方程的狹義相對論形式,用於描述自旋為...
緒論 定義 形式推導 自由粒子解波動方程或稱波方程 (英語:wave equations) 由麥克斯韋方程組導出的、描述電磁場波動特徵的一組微分方程,是一種重要的偏微分方程 ,主要描述...
波動方程介紹 方程形式 方程的解 要點分析 物理意義KdV方程是1895年由荷蘭數學家科特韋格(Korteweg)和德弗里斯(de Vries)在研究淺水中小振幅長波運動時共同發現的一種單向運動淺水波偏微...
