波包

波包，英文翻譯為wavepacket，一般的波是由若干種以至無限多種諧波疊加而成的，往往仍然是非局域性的。但是，在特定條件下，疊加後的波有可能是局域性的，猶如被某種曲面包裹住那樣。這種局域性的波就叫做“波包”。舉一個例子：取一根均勻而又較長的橡皮繩，讓它的一端固定在牆上或別的什麼上，另一端握在手中，拉直。起初，該系統處於靜止狀態。後來，握繩的手突然抖動了一下後又回到了原來的位置並重新靜止下來。此後就會看到繩上有一個隆起的形狀在移動，這個隆起的部分就叫做“波包”。 波包是波的一個特殊的品種，用以描述波包狀態的代數函式仍然叫做“波函式”。波包的局域性並不是很嚴格的。人們在收聽廣播時接收到的是電台發來的電磁波，電台總有停播的時候，所以這種電磁波肯定是局域性的，但習慣上不把這種局域性的波稱為波包。在量子力學裡，薛丁格所說的波包是指微觀粒子，其尺寸就是粒子的尺寸。如果用波函式來描述它，那么就會發現，波函式在任意大的範圍內都不會嚴格等於零。這時的所謂“局域”，實際上是指“主要分布區域”。從數學形式上看，k和x在波函數裡是處於完全平等的地位，所以波的概念不是坐標空間裡特有的。坐標空間的波在k空間裡(或動量空間裡)仍然是波，k空間裡也有波包。

基本信息

• 中文名：波包
• 英文名：wavepacket

• 特性：非局域性
• 速度：相速度、群速度

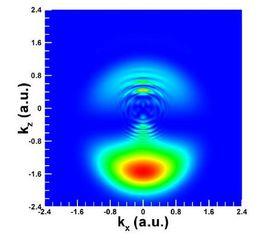
包含描述

波包的群速度和相速度

對於波包，描述其傳播的有兩個速度：相速度和群速度。

相速度

相速度是波的相位向前傳播的速度，如果一列波的波動方程為ψ = A cos(kx-ωt)，其等相面為“kx-ωt=常數”，對等相面微分可以知道dx/dt=ω/k，故其相速度為ω/k。由於組成波包是一系列簡諧波，因此除非這一系列波的相速度都相等(即不存在色散)，否則波包實際上是沒有嚴格確定的相速度的，但由於能夠組成波包的一系列波往往參數非常接近，所以通常可以將波包分解成簡諧波以後，按權重計算出平均相速度，當作波包的相速度。

群速度

考慮最簡單的兩列波疊加，一列為ψ = A cos(kx-ωt)，另一列為ψ' = A cos(k'x-ω't)，其中k'=k+dk，ω'=ω+dω，則由三角函式的和差公式可得出疊加後的波動方程為：

Ψ = 2A cos(xdk/2-tdω/2) cos[x(2k+dk)/2-t(2ω+dω)/2]

後一項約為cos(kx-ωt)，也就是相速度，而前一項的推進速度為dω/dk，它表示波的最大振幅處向前推進的速度，也就是群速度。

量子理論

在量子力學建立之初，波粒二象性被提出之後，對它的解釋曾有過很大的爭議。是否可以認為粒子就是波包呢？由於德布羅意關係λ=h/p，ν=E/h，若假設粒子就是波包，則組成粒子的群速度不僅不等於相速度，而且彼此之間的相速度也各不相同，造成波包在傳播過程中擴散，這意味著粒子會在運動中自動解體，這顯然是不合理的。後來玻恩提出的統計解釋認為，所謂的波表征的是粒子在空間中的各個位置出現的機率，波包的擴散實際上是粒子機率的擴散，而並非粒子本身的解體，這種解釋在一定程度上解決了波動性和粒子性的矛盾，目前為多數人所認同。