定義
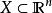 波前集
波前集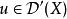 波前集
波前集 波前集
波前集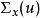 波前集
波前集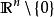 波前集
波前集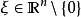 波前集
波前集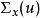 波前集
波前集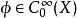 波前集
波前集 波前集
波前集 波前集
波前集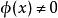 波前集
波前集 波前集
波前集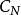 波前集
波前集在歐式空間的一個區域中,一個分布在一個點處的奇異纖維,作為的一個子集, 是在這一點所有奇異方向的余集。嚴格的定義用到傅立葉變換,不屬於若且唯若存在緊支集光滑函式以及的一個錐鄰域(在正實數乘法下不變)使得,並且在中有如下估計:對於任意正整數N ,存在正常數使得:
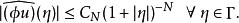 波前集
波前集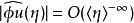 波前集
波前集(我們經常將這個估計寫為。)
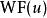 波前集
波前集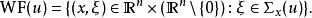 波前集
波前集f的波前集定義為:
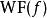 波前集
波前集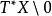 波前集
波前集由下面波前集在坐標變化下的性質,可以定義光滑流形X 上的分布 f的波前集為餘切叢去掉零截面的一個錐子集。
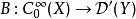 波前集
波前集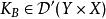 波前集
波前集如果有Schwarz核,定義為:
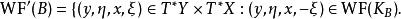 波前集
波前集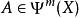 波前集
波前集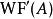 波前集
波前集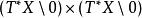 波前集
波前集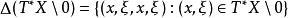 波前集
波前集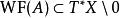 波前集
波前集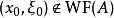 波前集
波前集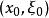 波前集
波前集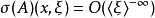 波前集
波前集對於擬微分運算元, 可以驗證包含於的對角線中。並且如果我們定義 如下:若且唯若在的一個錐鄰域中,A的象徵滿足估計。
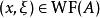 波前集
波前集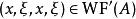 波前集
波前集那么我們有若且唯若。
等價定義
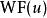 波前集
波前集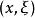 波前集
波前集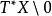 波前集
波前集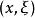 波前集
波前集 波前集
波前集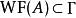 波前集
波前集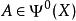 波前集
波前集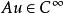 波前集
波前集Hormander最早的定義用到了擬微分運算元在分布上的作用:是所有滿足如下性質的點在中的補集: 存在的錐鄰域 使得對於任意的滿足的擬微分運算元, 有。
另一個有用的等價定義用到FBI變換。
性質
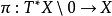 波前集
波前集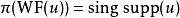 波前集
波前集(1) 如果記為餘切叢上自然投影,則。
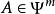 波前集
波前集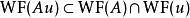 波前集
波前集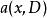 波前集
波前集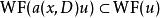 波前集
波前集(2) 對於擬微分運算元,。特別的,我們有對於任意的光滑係數微分運算元,。
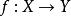 波前集
波前集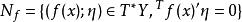 波前集
波前集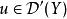 波前集
波前集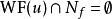 波前集
波前集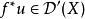 波前集
波前集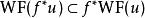 波前集
波前集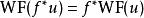 波前集
波前集(3) 如果是一個光滑映射,記為f 的法叢。如果滿足,那么我們可以“唯一的”定義u在f 下的拉回。並且我們有。 特別的,如果f是一個微分同胚,。所以波前集定義在餘切叢上是不取決於坐標的。
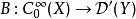 波前集
波前集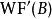 波前集
波前集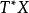 波前集
波前集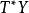 波前集
波前集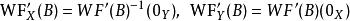 波前集
波前集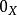 波前集
波前集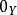 波前集
波前集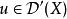 波前集
波前集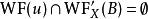 波前集
波前集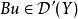 波前集
波前集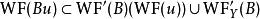 波前集
波前集(4)令如果將視作從到的一個關係,並且記。這裡和分別是X和Y上餘切叢的零截面。則如果滿足,那么我們可以“唯一的”定義。並且我們有。
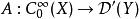 波前集
波前集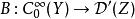 波前集
波前集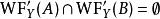 波前集
波前集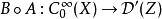 波前集
波前集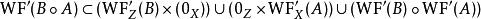 波前集
波前集(5)如果和滿足,那么我們可以“唯一的”定義複合運算元。並且我們有:。
這裡最後一項是將波前集視為關係下的複合。
套用及推廣
 波前集
波前集波前集可用於函式、振盪積分、余法分布、拉格朗日分布、分布的運算、擬微分運算元與微局部化以及奇異性的傳播。
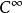 波前集
波前集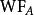 波前集
波前集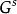 波前集
波前集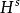 波前集
波前集以上所定義的波前集描述的是分布的關於正則性的奇異性,類似的可以定義關於實解析性的波前集,關於Gevery類的波前集,關於Sobolev空間的波前集等等。在使用FBI變換的定義中,這些波前集有一個很好的統一的描述。

