簡介
通常人們會使用冪級數展開式的形式來描述光學系統的像差。由於澤尼克多項式和光學檢測中觀測到的像差多項式的形式是一致的，因而它常常被用來描述波前特性。但這並不意味著澤尼克多項式就是用來擬合檢測數據的最佳多項式形式。在某些情況下，用澤尼克多項式來描述波前數據具有很大的局限性。比如說，當需要考慮空氣擾動的時候，澤尼克多項式幾乎沒有什麼價值。同樣地，我們也無法找到一組合適的澤尼克多項式來描述單點金剛石車削加工（single point diamond turning process）中的製造誤差。為了準確地描述圓錐面光學元件（conical optical elements）的對準誤差，必須對澤尼克多項式進行修正。盲目地使用澤尼克多項式來表達檢測數據只會導致糟糕的結果。
性質
澤尼克多項式是由無窮數量的多項式完全集組成的，它有兩個變數，ρ和θ，它在單位圓內部是連續正交的。需要注意的是，澤尼克多項式僅在單位圓的內部連續區域是正交的，通常在單位圓內部的離散的坐標上是不具備正交性質的。
澤尼克多項式具有三個和其他正交多項式集不一樣的性質。
1、澤尼克多項式Z(ρ, θ)可以被化解為徑向坐標ρ和角度坐標θ的函式，其形式如下：
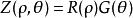澤尼克多項式這裡，關於角度的函式G(θ)是一個以2π弧度為周期的連續函式，並且滿足當坐標系旋轉α角度之後，其形式不發生改變，也就是旋轉不變性：
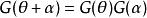澤尼克多項式其三角函式集形式如下：
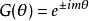澤尼克多項式這裡m是任意正整數或0。
2、澤尼克多項式的第二個性質是徑向函式R(ρ)必須是ρ的n次多項式，並且不包含冪次低於m次的ρ方項。
3、第三個性質是當m為偶數時R(ρ)也為偶函式，m為奇數時，R(ρ)也為奇函式。
徑向多項式R(ρ)可以看作是雅可比多項式（Jacobi polynomials）的特例，它們的正交和歸一化性質可由如下式子表示：
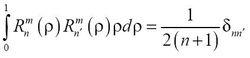澤尼克多項式
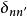澤尼克多項式
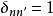澤尼克多項式
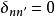澤尼克多項式上式中的 是克羅內克符號（Kronecker delta），即當n=n’時， ，當n≠n'時，, 。 並且它具有歸一化的性質：
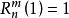澤尼克多項式在計算徑向多項式時，為了方便起見，我們通常會將其分解成如下形式：
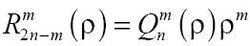澤尼克多項式
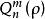澤尼克多項式其中 的次數為2(n-m)，由下式給出：
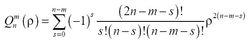澤尼克多項式通常我們會用實數形式的多項式（正弦和餘弦函式）來代替複製數多項式，這樣的話，波前像差函式W(ρ, θ)的澤尼克展開式就有如下形式：
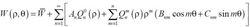澤尼克多項式澤尼克項
一般來說，給出的48項澤尼克項中，#0項是個常數或者說是平移項（piston term），這一項的係數也代表了平均光程差；而#1和#2項分別是x和y方向的傾斜項（tilt terms），#3代表了聚焦，因此，#1到#3項代表了波前的高斯或者近軸特性；#4和#5項代表了像散和離焦，#6和#7項代表彗差和傾斜，而#8項代表了3級像差和離焦，也就是說#4到#8項為3級相差項；同樣地，#9到#15項代表了5級像差，而#16到#24項代表了7級像差，#25到#35項代表了9級像差，#36到#48項代表了11級像差。
賽德爾像差
澤尼克多項式和賽德爾像差波前的初級和3級像差係數可以用澤尼克多項式來表示。我們將波前函式用澤尼克項的前九項來表示成如下形式：
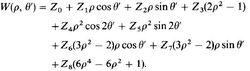澤尼克多項式這些澤尼克項和像差的對應關係如下：
Z平移；Zx軸傾斜；Zy軸傾斜；Z離焦；Z像散0度和離焦；Z像散45度和離焦；Z彗差和x軸傾斜；Z彗差和y軸傾斜；Z球差和離焦。
由於這些澤尼克項中與視場無關，它們並非真正的賽德爾像差。用干涉測試的方法智慧型得到單個視場點的波前數據。這使得場曲看上去像離焦，而畸變看上去像傾斜。因此，要得到賽德爾像差，就必須測量一定數量的視場點。
我們可以按照初級和3級像差的形式繼續改寫上述波前函式，也就是合併同類項，並用波前相差係數做等價替換，結果如下：
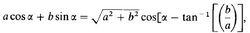澤尼克多項式便可得到如下所示的視場無關的波前相差係數：
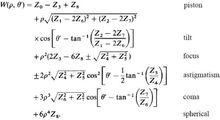澤尼克多項式下表列出了上述視場無關像差多項式的度量（Magnitude），符號和角度（Angle）。注意離焦項的符號選擇原則是使得其係數的數值最小，像散符號的選取則相反。
澤尼克多項式套用
光學主反射鏡是空問光學遙感器的組成部分，它的鏡面面形精度是影響空間光學遙感器解析度的重要因素之一。在地面裝調過程中，反射鏡在光軸水平和光軸豎直兩種狀態下，由於引力場的作用，反射鏡的鏡面將會發生變形，因此在進行光學反射鏡設計時需要做鏡面變形分析，以檢驗所設計的光學反射鏡是否滿足面形精度要求。鏡面變形包括剛體位移和表面變形，剛體位移會引起光學系統像傾斜、離軸和離焦，表面變形將影響光學系統的波前差。剛體位移可以通過調整光學元件之間的相對位置來消除，而表面變形無法消除。因此鏡面變形中的表面變形能夠真實反映光學反射鏡的面形精度。以自由曲面鏡面為例，通過有限元分析得到面形數據，用澤尼克多項式對變形後的面形進行精確擬合，並分離出剛體位移部分得到表面變形雲圖，計算出表面變形的表面變形均方根和表面變形最大值與最小值之差 。
