方程的敘述
泊松方程為
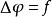 泊松方程
泊松方程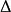 泊松方程
泊松方程 泊松方程
泊松方程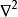 泊松方程
泊松方程在這裡 代表的是拉普拉斯運算元,而f和 可以是在流形上的實數或複數值的方程。當流形屬於歐幾里得空間,而拉普拉斯運算元通常表示為 ,因此泊松方程通常寫成
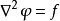 泊松方程
泊松方程在三維直角坐標系,可以寫成
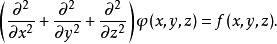 泊松方程
泊松方程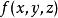 泊松方程
泊松方程如果有 恆等於0,這個方程就會變成一個齊次方程,這個方程稱作“拉普拉斯方程”。
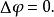 泊松方程
泊松方程泊松方程可以用格林函式來求解;如何利用格林函式來解泊松方程可以參考禁止泊松方程。現在有很多種數值解。像是鬆弛法,不斷迴圈的代數法,就是一個例子。
數學表達
通常泊松方程表示為
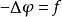 泊松方程
泊松方程 泊松方程
泊松方程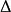 泊松方程
泊松方程這裡代表拉普拉斯運算元,f為已知函式,而為未知函式。當 f=0時,這個方程被稱為拉普拉斯方程。
為了解泊松方程我們需要更多的信息,比如狄利克雷邊界條件:
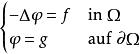 泊松方程
泊松方程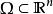 泊松方程
泊松方程其中 為有界開集。
這種情況下利用基礎函式構建泊松方程的解,拉普拉斯方程的基礎函式為:
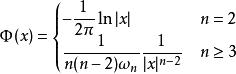 泊松方程
泊松方程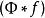 泊松方程
泊松方程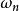 泊松方程
泊松方程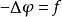 泊松方程
泊松方程其中 為n維歐幾里得空間中單位球面的體積,此時可通過卷積得到 的解。
為了使方程滿足上述邊界條件,我們使用格林函式
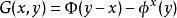 泊松方程
泊松方程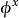 泊松方程
泊松方程為一個校正函式,它滿足
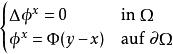 泊松方程
泊松方程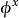 泊松方程
泊松方程 泊松方程
泊松方程通常情況下 是依賴於 。
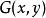 泊松方程
泊松方程通過 可以給出上述邊界條件的解
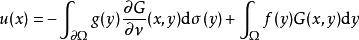 泊松方程
泊松方程 泊松方程
泊松方程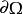 泊松方程
泊松方程其中 表示 上的曲面測度。
此方程的解也可通過變分法得到。
套用
在靜電學很容易遇到泊松方程。對於給定的 f找出φ是一個很實際的問題,因為我們經常遇到給定電荷密度然後找出電場的問題。在國際單位制(SI)中:
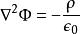 泊松方程
泊松方程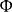 泊松方程
泊松方程 泊松方程
泊松方程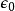 泊松方程
泊松方程此 代表電勢(單位為伏特), 是電荷體密度(單位為庫侖/立方米),而 是真空電容率(單位為法拉/米)。
如果空間中有某區域沒有帶電粒子,則
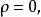 泊松方程
泊松方程此方程就變成拉普拉斯方程:
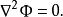 泊松方程
泊松方程高斯電荷分布的電場
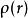 泊松方程
泊松方程如果有一個三維球對稱的高斯分布電荷密度 :
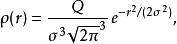 泊松方程
泊松方程此處, Q代表總電荷
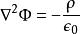 泊松方程
泊松方程此泊松方程: 的解Φ( r)則為
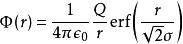 泊松方程
泊松方程erf( x)代表的是誤差函式。
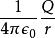 泊松方程
泊松方程注意:如果 r遠大於σ,erf( x)趨近於1,而電場Φ( r)趨近點電荷電場 ;正如我們所預期的。

