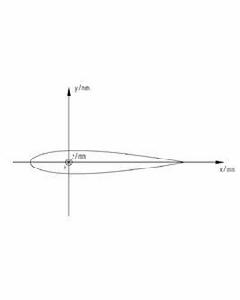
內容
翼型表面的力:翼型在流場中所受的力是作用在上下翼面的分布力的合力,分布力有兩種:一種是法向 力,即壓力;另一種是切向力,即摩擦力。但在理論計算中由於切向的摩擦力微乎其微,所以一般忽略不計。同時,定義和遠前方來流相垂直的合力為升力L,與遠前方來流方向一致的合力為阻力D
俯仰力矩:由理論力學可知,平面力系可以合成到作用在某個指定點上的一個力和一個力矩,所以沿翼面分布的法向力(壓力)也可以合成為一個力和一個力矩,這個力矩命名為俯仰力矩。
在一定的雷諾數下,不論迎角是多少,每次都將力系合成到一個特殊的點,使得這一點的俯仰力矩都一樣大,那么這個點就叫做氣動中心點,又稱作焦點。
重點
關於氣動中心的概念有兩個重點:
氣動中心與壓力中心不同:壓力中心是力系合成到一個特殊點時,使得這個點的合力矩為0的點,壓力中心在氣動中心的後面;而氣動中心是使得合力矩不變的點。壓力中心的位置隨著迎角的改變而改變,當迎角增大,升力增大,壓力中心前移,這同時使得壓力中心與氣動中心的距離縮短,增大的升力與縮短力臂乘積剛好是不變的力矩,這也正是氣動中心的定義所要求的。
不同雷諾數、不同翼型氣動中心位置不一樣:翼型準確的氣動中心位置主要是通過實驗測得的,在一些比較全的翼型書中會標有“a.c.position”的字樣,同時在下面列舉了不同雷諾數所對應的氣動中心位置。這些氣動中心的位置在不同雷諾數下各不相同,且在垂直弦長方向上並不為0,但在一般的葉片設計、氣動模擬計算中,對應雷諾數和翼型的氣動中心位置數據不一定能找到,所以將氣動中心位置取為弦長1/4處是可以接受的。
1.氣動中心與壓力中心不同:壓力中心是力系合成到一個特殊點時,使得這個點的合力矩為0的點,壓力中心在氣動中心的後面;而氣動中心是使得合力矩不變的點。壓力中心的位置隨著迎角的改變而改變,當迎角增大,升力增大,壓力中心前移,這同時使得壓力中心與氣動中心的距離縮短,增大的升力與縮短力臂乘積剛好是不變的力矩,這也正是氣動中心的定義所要求的。
2.不同雷諾數、不同翼型氣動中心位置不一樣:翼型準確的氣動中心位置主要是通過實驗測得的,在一些比較全的翼型書中會標有“a.c.position”的字樣,同時在下面列舉了不同雷諾數所對應的氣動中心位置。這些氣動中心的位置在不同雷諾數下各不相同,且在垂直弦長方向上並不為0,但在一般的葉片設計、氣動模擬計算中,對應雷諾數和翼型的氣動中心位置數據不一定能找到,所以將氣動中心位置取為弦長1/4處是可以接受的。
依據
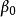 氣動中心
氣動中心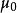 氣動中心
氣動中心採用中弧線坐標 和 表示氣動合力對翼型前緣點a的力矩係數:
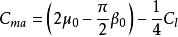 氣動中心
氣動中心換算到1/4弦長處的氣動中心取矩,得
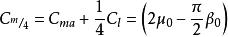 氣動中心
氣動中心在氣動中心處的力矩係數公式中沒有迎角,說明其關於迎角是一個常數,且即便在升力為0的情況下仍有此力矩,這個力矩稱作剩餘力矩,又作零升力力矩。無論迎角多大,只要對氣動中心取矩,其值都等於這個剩餘力矩。
套用
風力機變槳調節時,為了避免葉片變槳時氣動合力對變槳軸產生交變應力,通常在葉片設計時就將不同翼剖面處翼型的氣動中心連線作為葉片的變槳軸,這樣做可以在一定程度上避免疲勞破壞,並且對於變槳精度控制也有益處。
在航空領域中,氣動中心的相關理論對於飛機俯仰穩定性設計也有一定幫助。