概念
遊程檢驗亦稱“連貫檢驗”，是根據樣本標誌表現排列所形成的遊程的多少進行判斷的檢驗方法。
例1：設某樣本n=12人的標誌表現為男、女，有以下三種排列。
(i) 男\男，女\女\女，男，女\女，男\男\男\男；
(ii) 男\男\男\男\男\男\男，女\女\女\女\女；
(iii) 男，女，男，女，男，女，男，女，男，女，男\男；
連續出現男或女的區段稱為遊程。
例2：00110111000100100010
首先看零在這個序列中出現幾次，假如有一個零，也算一次，一百個零連在一起也算一次，這個一次稱作一個遊程。查一查零共出現六次，所以有六個零的遊程。其他以此類推。
在例1中，第一組的遊程是5，第二組的遊程是2，第三組的遊程是11。
這裡需要知道遊程檢驗的原則：如果序列為真隨機序列，那么遊程的總數應該不太多也不太少。如果遊程的總數極少，就說明樣本缺乏獨立性，內部存在一定的趨勢或者結構，這可能由於觀察值間不獨立，或者來自不同的總體。如果樣本間存在大量遊程，則可能有系統的短周期波動影響觀察結果。同樣認為序列非隨機。從例1中可以看出，（i）是隨機性序列；（ii）（iii）是非隨機性序列，所以，可以用遊程的個數來檢驗樣本的隨機性，或總體的分布特徵。
本質
遊程檢驗的本質：首先，變數的類型必須為二分變數，例如性別變數，只有二個數組成的變數。然後，遊程檢驗的分析目的是用於判斷觀察值的順序是否隨機。這一點非常重要，因為，許多遇到的實際問題中並不只是使研究者關心分布的位置或者形狀，也包括樣本的隨機性。如果樣本不是從總體中隨機抽取的，則所做的任何推斷都將沒有價值。遊程檢驗是最簡單的判斷隨機性的方法。
方法
遊程檢驗的方法主要有以下3種：
1、檢驗總體分布是否相同
將從兩個總體中獨立抽取的兩個樣本的觀察值混合後，觀察遊程個數，進行比較。
2、檢驗樣本的隨機性
將取自某一總體的樣本的觀察值按從小到大順序排列，找出中位數（或平均數），分為大於中位數的小於中位數的兩個部分。用上下交錯形成的遊程個數來檢驗樣本是否是隨機的。
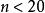遊程檢驗3、檢驗規則（小樣本： ）
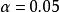遊程檢驗
遊程檢驗套用表La和Lb，( ， 為臨界值)
（1）單側檢驗：
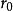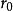遊程檢驗 遊程檢驗
遊程檢驗 遊程檢驗觀察到的遊程個數 ≤臨界值（La表）或 ≥臨界值（Lb表），否定 ；反之，接受 。
（2）雙側檢驗：
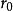遊程檢驗觀察到的遊程個數
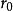遊程檢驗 遊程檢驗 遊程檢驗 遊程檢驗 遊程檢驗(La)< < (Lb)，接受 下限，上限反之，拒絕
4、大樣本（ n或 n大於20）
遊程個數r近似常態分配，檢驗統計量：
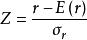遊程檢驗其中：
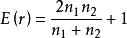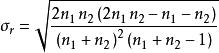遊程檢驗
遊程檢驗分別代表均值和方差，當n、n很大的時候，Z近似服從標準常態分配。
非參數檢驗
亦稱無分布檢驗、分布自由檢驗。非參數假設的檢驗準則。常用非參數檢驗有：基於實際觀測頻數與理論期望頻數直接比較的皮爾遜χ 檢驗；基於經驗分布函式和理論分布函式或二經驗分布函式之差的柯爾莫戈洛夫檢驗、斯米爾諾夫檢驗、倫尼檢驗、W 檢驗、ω 檢驗、V檢驗；基於順序統計或秩統計量的符號檢驗、秩檢驗、遊程檢驗以及其他一些快速和簡便非參數檢驗方法。
非參數檢驗方法的特點是，1. 不受或很少受總體具體分布形式的影響，故適應性十分廣泛；2. 由於不 能充分利用總體信息，方法的針對性往往較差、功效往往較低；3. 非參數檢驗的統計量的精確分布，只在極 個別場合可以掌握，因此非參數檢驗一般要求較大的 樣本容量。
非參數檢驗主要用於：1. 處理非正態數據；2. 處 理用等級(秩)度量的統計資料；3. 對參數檢驗進行 驗證； 4. 獲得 “快速”或 “簡便” 的檢驗方法。
