定義
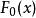 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗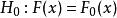 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗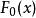 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗哥洛夫(Kolmogolov)1933年證明了著名的柯爾莫哥洛夫定理(隨機變數的存在性定理),並由此建立了一個分布擬合檢驗——柯爾莫哥洛夫檢驗,用於檢驗完全已知的連續型分布函式 : ( 為完全已知的連續型分布函式)。
 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗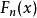 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗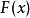 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗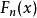 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗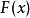 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗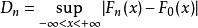 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗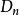 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗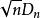 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗由格里汶科(Glivenko)定理知,當樣本容量n充分大時,經驗分布函式 與理論分布函式 相當接近。所以,當 成立且n較大時, 與 的差距不應太大,故用統計量 作為的檢驗統計量,並導出了的精確分布和的極限分布。
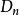 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗給出的具體求法和拒絕域的確定方法:
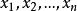 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗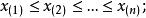 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗(1)將樣本觀測值 ,按不降次序排列成
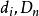 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗(2)計算 的值:
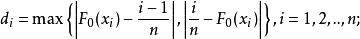 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗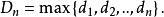 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗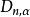 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗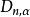 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗(3)對給定的顯著性水平 ,當n≤100時,在柯爾莫哥洛夫檢驗的臨界值 表中查臨界值 ;
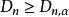 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗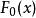 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗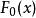 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗(4)若 ,則拒絕原假設 ,即認為樣本不是取自分布為 的總體;否則接受 ,即認為樣本取自分布為 的總體。
 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗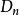 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗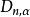 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗與皮爾遜 擬合檢驗法相比,該檢驗法充分利用樣本所提供的信息,在所有點上考慮了經驗分布函式與總體分布函式之間的差異,克服了 擬合檢驗依賴於區問的劃分的缺點。但是,只有當總體為一維且理論分布完全已知時,柯爾莫哥洛夫檢驗優於 擬合檢驗。當理論分布中含有未知參數時,柯爾莫哥洛夫檢驗需要做特殊處理,只對常態分配和指數分布做了這樣的處理。且當樣本容量n>100時,或樣本觀測值中有重複數據時,統計量 的求法及臨界值 的求法還要另作處理。
正態性檢驗
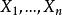 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗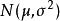 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗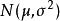 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗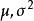 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗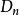 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗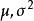 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗要通過樣本 來檢驗總體的分布是否服從常態分配 .由 於中有兩個未知參數 ,不能直接用Kolmogolov統計量 來檢驗常態分配的假設.對未知參數 ,如用其無偏估計量
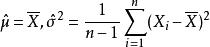 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗代替,則要檢驗的假設實際上是
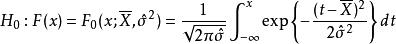 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗與Kolmogolov統計量類似取檢驗統計量為
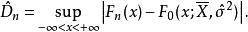 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗對給定的顯著性水平 ,檢驗規則為:
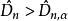 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗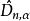 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗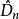 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗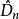 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗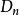 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗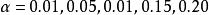 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗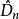 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗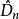 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗若 ,則拒絕 ,否則就接受 .為求 ,需要知道 的分布函式,顯然 的分布不同於 的分布。對於 ,Lilliefors計算了 的臨界值 。
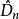 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗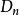 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗值的計算方法與 值的計算方法相同。
指數分布的檢驗
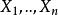 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗要通過樣本 檢驗總體的分布是否服從單參數指數分布,一般的參數指數分布函式
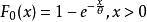 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗中,有一個未知參數 ,如用 的極大似然估計
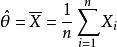 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗代替 ,則要檢驗的假設實際上是
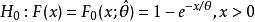 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗與柯氏檢驗類似,可取檢驗統計量
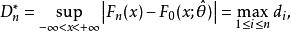 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗其中
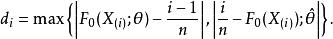 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗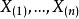 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗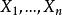 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗是 的順序統計量,當樣本中有重複數據時,與前面一中的求法相同。
 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗為提高檢驗的功效,1971年Finklestein和Sehafer提出檢驗 的統計量為
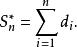 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗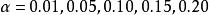 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗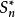 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗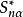 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗並對 ,求出了 的臨界值 的表。
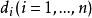 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗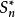 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗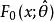 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗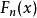 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗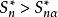 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗 柯爾莫哥洛夫檢驗
柯爾莫哥洛夫檢驗顯然, 值大, 的值也大,此時分布函式 的曲線與經驗分布函式 的曲線擬合的不好,應拒絕 .所以對顯著性水平 ,檢驗的規則為:若 時,拒絕 ,否則就接受 。
