定義
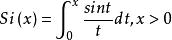正弦積分正弦積分函式的定義為：，本函式採用勒讓德-高斯求積公式計算該積分。
正弦積分函式表
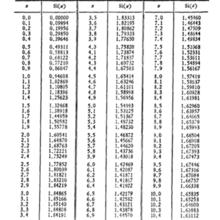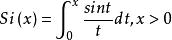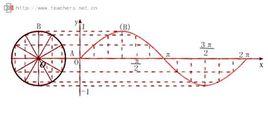
正弦積分函式表 正弦積分，函式表如右圖所示
正弦積分函式圖像
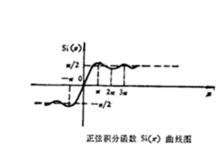正弦積分函式圖像正弦積分函式圖像如右圖所示
有圖像可得正弦積分函式的性質有：
（1）Si(x)為奇函式，即Si(-x)=-Si(x)；
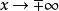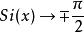正弦積分
正弦積分（2）當時，則；
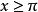正弦積分
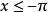正弦積分 正弦積分
正弦積分（3）在的區間內，當x=奇數倍時，Si(x)有極大值；當x=偶數倍時，Si(x)有極小值。在的區間內，情況基本相同，只是多了一個負號 。
正弦積分的計算
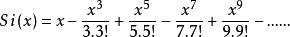正弦積分求
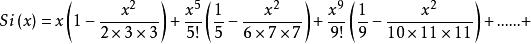正弦積分上式是一個麥克勞林冪級數展開式，此式形式簡單，推倒容易，使用方便，但可以改寫為：
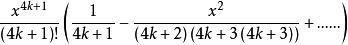正弦積分式中，k=0,1,2，......
上式所表示的無窮級數肯定是收斂的，越後面的項絕對值越小。如果它已經小於一個很小的正整數
正弦積分 正弦積分，則不必再算了。這個就稱作截止量。
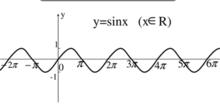弦函式圖像眾所周知，不管哪種型號的計算機都會有捨入誤差，所以使用 上述公式計算Si(x)時都有一定的精度。實驗數值結果表明，字長為48位的計算機，只要x小於23就可以套用。字長為32位的計算機， x小於10還是保險的。
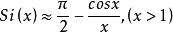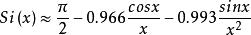正弦積分
正弦積分當自變數超過23時,有一個如下形式的常用近似式，],使用該式,當x值變大時,精度有所提高.但只能滿足小數點後兩位需建立一個較高精度的經驗公式：。
