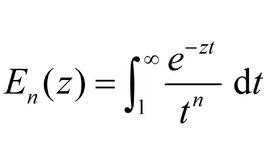指數積分的定義
n階指數積分(Exponential Integral)為
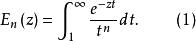 指數積分
指數積分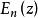 指數積分
指數積分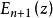 指數積分
指數積分對正整數n≥1, 與 之間的遞推關係為
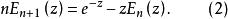 指數積分
指數積分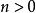 指數積分
指數積分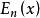 指數積分
指數積分當自變數為正實數且 時,函式 滿足如下不等式
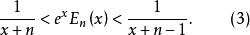 指數積分
指數積分一階指數積分
 指數積分
指數積分一階指數積分(虛數自變數)是自變數取純虛數時的積分(即式(1)中 )
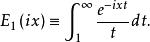 指數積分
指數積分該式也可以表示為如下等效形式
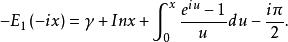 指數積分
指數積分 指數積分
指數積分式中: 為歐拉一馬歇羅尼常數(Euler-Mascheroni constant):
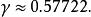 指數積分
指數積分三階指數積分
三階指數積分(實數自變數)是自變數為正實數的指數積分(即式(1)中n=3)為
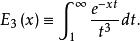 指數積分
指數積分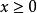 指數積分
指數積分這一函式可用來計算無限片狀分布聲源的輻射噪聲場。對所有 都有效的一個近似式(基於式(3))為
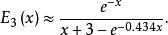 指數積分
指數積分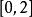 指數積分
指數積分對於在區間 上取值的x,此近似式的最大相對誤差為2%。
正弦積分函式與餘弦積分函式
正弦積分函式(Sine Integral Function)與餘弦積分函式(Cosine Integral Function)分別為
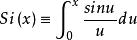 指數積分
指數積分和
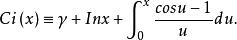 指數積分
指數積分這兩個函式與指數積分的關係如下
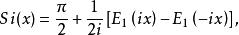 指數積分
指數積分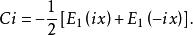 指數積分
指數積分由此可得
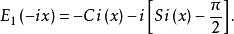 指數積分
指數積分這兩個函式的漸近值為
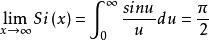 指數積分
指數積分和
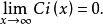 指數積分
指數積分指數積分與其它函式的關係
與對數積分
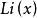 指數積分
指數積分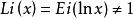 指數積分
指數積分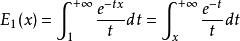 指數積分
指數積分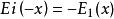 指數積分
指數積分指數積分與對數積分 的關係: ;另外一個有密切關係的函式: ;可以延伸到負數: ;我們可以把兩個函式都用整函式來表示:
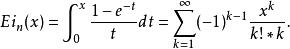 指數積分
指數積分此函式的性質:
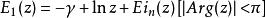 指數積分
指數積分;
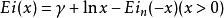 指數積分
指數積分;
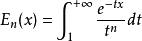 指數積分
指數積分指數積分還可以推廣為: 。
導數
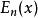 指數積分
指數積分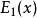 指數積分
指數積分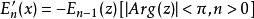 指數積分
指數積分函式 與 的導數有以下簡單的關係: ;然而,這裡假設了n是整數;複數n的推廣還沒有在文獻中報導,雖然這種推廣是有可能的。
復變數的指數積分
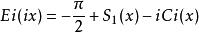 指數積分
指數積分從定義中可以看出,指數積分與三角積分之間的關係: 。