簡介
任何複雜信號——例如音樂信號,都可以通過傅立葉變換分解為許多頻率不同、幅度不等的正弦信號的迭加。在電路理論中也涉及到許多正弦信號的知識,可將其稱為電壓或電流。
一個正弦信號可表示為 x( t) = Asin( ω* t+ φ)= Acos( ω* t+ φ-π/2) 。式中, A 為振幅, ω為角頻率(弧度/秒), φ 為初始相角(弧度)。正弦信號是周期信號,其周期 T為: T=2π/ ω=1/ f 。
由於餘弦信號與正弦信號只是在相位上相差π/2,所以將它們統稱為正弦型信號(簡稱正弦信號)。工業及照明用電就是正弦信號。
振盪電路輸出的正弦波一般都含有諧波分量,方波就是由一系列的諧波分量疊加而成。
表達式
x( t) = Asin( ω* t+ φ)= Acos( ω* t+ φ-π/2)
其中: A為振幅, ω為角頻率(弧度/秒), φ為初始相角(弧度)。這三個參量稱為正弦信號的三要素。
除了這三個要素,正弦信號還有周期和頻率兩個參數,他們之間的關係為: T=2π/ ω=1/ f 。
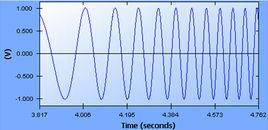
 正弦信號圖
正弦信號圖有用的性質
正弦信號作為一種基本信號,它具有非常有用的性質:
1. 兩個同頻率的正弦信號相加,雖然它們的振幅與相位各不相同,但相加的結果仍然是原頻率的正弦信號。
2. 如果有一個正弦信號的頻率 f1 等於另一個正弦信號頻率 f的整數倍,即 f1 = nf,則其合成信號是非正弦周期信號,其周期等於基波(上面那個頻率為 f的正弦信號就稱作基波)的周期 T= 1/ f ,也就是說合成信號是頻率與基波相同的 非正弦信號。
3. 正弦信號對時間的微分與積分仍然是同頻率的正弦信號。
以上這些優點給運算帶來了許多方便,因而正弦信號在實際中作為典型信號或測試信號而獲得廣泛套用。