定義
線性時不變動態電路在角頻率為 ω的正弦電壓源或電流源激勵下，隨著時間的增長，當暫態回響消失，只剩下正弦穩態回響，電路中全部電壓電流都是角頻率為 ω的正弦波時，稱電路處於正弦穩態。滿足這類條件的動態電路通常稱為正弦電流電路或正弦穩態電路。
意義
分析正弦穩態的重要性在於：
1. 很多實際電路都工作於正弦穩態。例如電力系統的大多數電路。
2. 用相量法分析正弦穩態十分有效。
3. 已知線性動態電路的正弦穩態回響，可以得到任意波形信號激勵下的回響。
優點
用相量法分析正弦穩態回響的優點有：
1. 不需要列出並求解電路的 n階微分方程。
2. 可以用分析電阻電路的各種方法和類似公式來分析正弦穩態電路。
3.讀者採用所熟悉的求解線性代數方程的方法，就能求得正弦電壓電流的相量以及它們的瞬時值表達式。
4. 便於讀者使用計算器和計算機等計算工具來輔助電路分析。
向量分析方法
分析正弦穩態的有效方法是相量法，相量法的基礎是用一個稱為相量的向量或複數來表示正弦電壓和電流。
用相量法求解電路正弦穩態回響的 方法和步驟如下：
1. 畫出電路的相量模型，用相量形式的KCL，KVL和VCR直接列出電路的復係數代數方程。
2. 求解復係數代數方程得到所感興趣的各個電壓和電流的相量表達式。
3. 根據所得到的各個相量，寫出相應的電壓和電流的瞬時值表達式。
1）網孔電流法
其主要以網孔電流相量為求解變數列方程組來求解，列方程時，方法同電阻電路不同的是，要利用自阻抗、互阻抗和電流的相量。
2）節點分析法
以節點電壓相量為求解變數列方程求解，列方程的方法同電阻電路，不同的是要利用自電導、互電導和電壓相量。
3）電源變換及戴維南定理的套用
一個電壓源與一個阻抗串聯的電路可以等效為一個電流源與一個阻抗並聯的並聯的電路。
含源二端網路的等效電路為戴維南等效電路，即等效為開路電壓U和等效阻抗Z串聯；也可以等效為短路電流I和等效阻抗Z並聯，即為諾頓等效電路。
4）相量圖法
相量圖法是通過做電流電壓的相量圖，求得未知相量。畫相量圖時要選擇參考向量，令該相量的初相為零。通常，對於串聯電路選電流相量作為參考相量，對於並聯電路，選電壓相量為參考相量。從參考相量出發，利用元件電壓與電流關係，即基爾霍夫電壓定律，基爾霍夫電流定律，確定有關電流與電壓間的相量關係，定性畫出相量圖，利用相量圖表示的幾何關係，求得所需的電流、電壓相量。
5）正弦穩態的疊加
在電路中，若各激勵源的頻率不同，只能用疊加法來求。要分別作出各個頻率電源作用時對應的相量模型，求出對應的相量，再寫出瞬時值，將瞬時值疊加。
激勵為非正弦周期信號f(t)可以將其表示為傅立葉級數，然後利用疊加定理求回響。
諧振電路
含有電阻、電感和電容原件而不含獨立電源的二端網路的性質可分為電阻性質，電感性質，電容性質3種。像這樣的二端網路，一般情況下不會是電阻性的，但在某一電源頻率上，出現連線埠電壓和電流的相位相同的情況時，即二端網路表現為電阻性的現象，稱諧振現象。此時的頻率成為諧振頻率，又稱為電路的固有頻率，它是由網路的結構和電容、電感的參數決定的。能發生諧振的電路，成為諧振電路（Resonant Circuit)。RLC串聯及並聯電路是兩種典型的諧振電路。
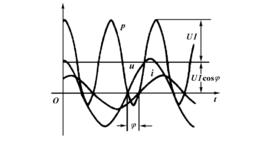
功率
工作在正弦穩態下負載的瞬時功率：
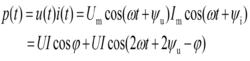正弦穩態瞬時功率平均功率：
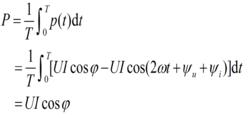正弦穩態平均功率由此式看出正弦穩態的平均功率不僅與電壓電流有效值乘積 UI有關，還與電壓電流的相位差 j= yu- yi有關，式中的因子cos j稱為功率因數。平均功率是一個重要的概念，得到廣泛使用，通常說某個家用電器消耗多少瓦的功率，就是指它的平均功率，簡稱為功率。
在實際生產與生活中大多電氣設備均為感性負載，它們的功率因數都比較低，這樣不能充分利用電源設備的容量，因此需要提高功率因數時常用的方法是在感性負載兩端並聯電容器。
