定義
 連續時間信號
連續時間信號 連續時間信號
連續時間信號信號的波形特徵可用兩個物理量來表示,即時間和幅值。將時間自變數 在除個別不連續點外的其他定義範圍內,任意時刻幅值都有定義的信號,稱為連續時間信號,一般用函式 表示 。由於“連續”是相對時間而言的,故連續時間信號的幅值可以是連續的,也可以是離散的。幅值連續是指在某一取值範圍內,信號可以取無限多個值。
特點及分類
連續時間信號
連續時間信號的特點是:除個別不連續點外,信號在所討論的時間段內的任意時間點都有確定的函式值(幅值),該函式值可以是連續的也可以是離散化的。
 連續時間信號
連續時間信號若信號的時間與幅值都是連續的,則稱此類信號為模擬信號。例如:信號 的時間和幅值都是連續的,即為模擬信號。如果信號的時間連續,但是信號的幅值離散,則稱此類信號為量化信號 。
離散時間信號
與連續時間信號相對的是離散時間信號。離散時間信號就是信號只在離散時間瞬間才有定義,簡稱離散信號,離散信號也常稱為序列。此處"離散"是指在某些不連續的時間瞬間給出函式值,在其它時間沒有定義。離散信號的幅值可以是連續的,也可以是離散的。若離散信號的幅值是連續的,則也可稱此類信號為抽樣信號或取樣信號。若離散信號的取值是離散的,則可稱此類信號為數位訊號 。
所以,有兩種連續信號:一種是取值也是連續的,一種是取值是離散的;同理,離散信號也有兩種:一種是取值連續——抽樣信號,一種是取值離散——數位訊號。
周期信號和非周期信號
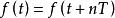 連續時間信號
連續時間信號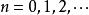 連續時間信號
連續時間信號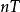 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號若信號按照一定的時間間隔周而復始,並且無始無終,則稱此類信號為周期信號。他們的表達式可以寫作
,(任意整數)其中稱為的周期,而滿足關係式的最小值則稱為是信號的基本周期。
若信號在時間上不具有周而復始的特性,即周期信號的周期趨於無限大,則稱此類信號為非周期信號。
連續時間信號和離散時間信號與周期信號和非周期信號彼此包含,即連續時間信號和離散時間信號中有周期信號和非周期信號,同理,周期信號和非周期信號中也包含連續時間信號和離散時間信號 。
典型信號
數學中很多常用的信號都是連續時間信號,下面主要介紹幾種典型的連續時間信號。
正弦信號
 連續時間信號
連續時間信號兩個振幅和初相位均不同的同頻率正弦信號相加後,其結果仍是原頻率的正弦信號。
抽樣信號
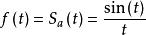 連續時間信號
連續時間信號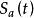 連續時間信號
連續時間信號 連續時間信號
連續時間信號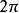 連續時間信號
連續時間信號 連續時間信號
連續時間信號是關於 的偶函式,是一個以 為周期,且具有 的單調衰減幅值的振盪信號 。
單位階躍信號
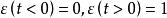 連續時間信號
連續時間信號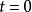 連續時間信號
連續時間信號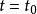 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號在躍變點 處,函式值未定義。若單位階躍信號的躍變點在 處,則稱其為延時單位階躍信號,其波形為 在時間軸 上向右平移 。
階躍信號可以表示任意的方波脈衝信號 。
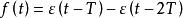 連續時間信號
連續時間信號單位衝激信號
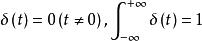 連續時間信號
連續時間信號單位衝擊信號的物理意義:持續時間無窮小,瞬間幅值無窮大,涵蓋面積恆為1 。衝擊信號與階躍信號的關係是:
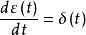 連續時間信號
連續時間信號衝擊偶信號是對單位衝擊信號求導所得,即
 連續時間信號
連續時間信號指數信號
指數信號根據其表達式中是否存在複數,可以將信號分為實指數信號和復指數信號。
1、實指數信號
 連續時間信號
連續時間信號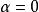 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號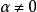 連續時間信號
連續時間信號 連續時間信號
連續時間信號若 ,則 ,即一條幅值為 且平行於時間軸 的直線,表示直流信號 。下面給出了 時實指數信號 的波形圖。
2、復指數信號
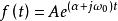 連續時間信號
連續時間信號 連續時間信號
連續時間信號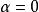 連續時間信號
連續時間信號 連續時間信號
連續時間信號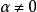 連續時間信號
連續時間信號 連續時間信號
連續時間信號由歐拉公式可得: 。若 ,則 變為正弦信號。下面給出了 時對應的復指數信號 的波形圖。
符號信號
 連續時間信號
連續時間信號符號信號與單位階躍信號的關係是:
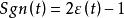 連續時間信號
連續時間信號基本運算
連續時間信號的基本運算主要有:加減法、乘法、微分、積分、時移、翻轉、尺度變換、信號分解、卷積等。
加法與乘法
連續時間信號的相加(或相乘)是指兩個信號在任意時刻函式值之和(或積)。需要注意的是:運算應在對應的時間上進行。
微分與積分
 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號信號 的微分(導數)是指信號 的函式值隨時間變化的變化率。當信號 中含有不連續點時,則 在這些不連續點上出現衝激,其強度為原函式在該點處的跳變數。
 連續時間信號
連續時間信號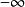 連續時間信號
連續時間信號 連續時間信號
連續時間信號信號 的積分是指在 到 區間內的任意時刻處,信號與時間軸所包圍的面積。
時移與翻轉
 連續時間信號
連續時間信號 連續時間信號
連續時間信號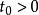 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號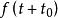 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號信號 時移 ( ),就是將 表達式及其定義域中所有自變數 替換為 ,從而使 表達式變為 。從信號波形上看, 的波形是將 的波形向左移動 時間; 的波形是將 的波形向右移動 時間。
 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號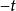 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號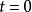 連續時間信號
連續時間信號信號 的翻轉就是將 表達式以及定義域中的所有自變數 替換為 ,從而使 的表達式變為 。從信號波形上看, 的波形與 的波形關於縱軸 呈鏡像對稱。
 連續時間信號
連續時間信號 連續時間信號
連續時間信號翻轉信號 的時移規律與信號 恰好相反 。
尺度變換
 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號信號 的尺度變換就是將信號 表達式中以及定義域中的所有自變數 替換為 ,從而使 的表達式變為 。
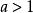 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號當 時, 是將 的波形沿時間軸壓縮至原來的 ;
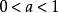 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號當 時, 是將 的波形沿時間軸擴展至原來的 ;
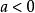 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號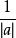 連續時間信號
連續時間信號當 時, 是將 的波形沿時間軸壓縮或擴展至原來的 。
信號分解
 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號信號 的分解就是將時間信號 用若干個奇異函式之和來表示。 可以分解任意信號 。
卷積
由卷積定義可知:
 連續時間信號
連續時間信號連續時間信號的卷積步驟 :
 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號 連續時間信號
連續時間信號(1) 將信號 和 中的自變數 變為 ,稱為函式的自變數;
(2) 把其中一個信號翻轉、平移;
 連續時間信號
連續時間信號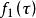 連續時間信號
連續時間信號 連續時間信號
連續時間信號(3) 將 和 相乘,對乘後的圖形積分。

