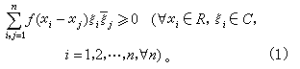正文
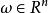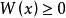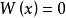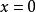正定函式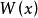 
正定函式 
正定函式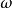 
正定函式 
正定函式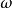 
正定函式 正定函式 數學定義：若在 上 ，且 僅有零解 ，稱函式 在 上正定。其中， 是包含原點的n維子集。
指實軸R上定義的滿足如下條件的連續函式?：這裡"正定"名稱來源於正定矩陣。事實上,式(1)等價於說,對一切n與一切點列,複數矩陣是一個正定矩陣（嚴格地說是半正定矩陣）。
正定函式概念的提出晚於它的一個同類，即所謂正定序列。O.特普利茨於20世紀初首先定義了正定序列的概念,即它是使矩陣正定的序列。G.赫格洛茨隨後發現了正定序列的一個非常重要的性質。正是在此基礎上,S.博赫納於30年代初得到了R上正定函式的重要性質，並第一個認識到了這個概念的重要性。他在這方面的重要貢獻之一便是建立了類似赫格洛茨定理的下述結果:R上連續函式?(x)是正定的，若且唯若存在有界增函式φ(t)，使
(2)
正定函式的概念可以允許下述推廣。首先,函式?的定義域可以不必是R，而是任意的局部緊T2群G。正定函式的概念推廣到這樣的群上是直接的。也就是說,G上連續函式?稱為是正定的（記其全體為p(G)），若
(1)'
在這樣的推廣下，正定序列與正定函式的概念便獲得了統一：前者是整數群Z上的正定函式，後者是實軸群R上的正定函式。正定函式概念的第二個推廣是函式?可以不必是連續的，而只要求是可測的（這裡可測性是關於所在群G的哈爾測度）。正如F.（F.）里斯、I.E.西格爾與J.馮·諾伊曼等先後指出的，這樣的正定函式與連續的正定函式只相差一個局部零（即在任意緊集上都幾乎處處為零）的正定函式。第三個推廣是將式 (1)（或（1）'）左邊的和改為積分。仍以R為例。R上波萊爾可測函式?稱為正定的，如果對一切φ∈L1（R），總有?(x-y)φ(x)徰(y)∈L1(R×R),且
(3)
可以證明，式(3)意義下的正定函式與式(1)意義下的正定函式是幾乎處處相等的。特別地，兩種意義下連續的正定函式的集合是一樣的。
正定函式是一個在許多領域都會遇到並且很有用的概念。如機率論中隨機變數的特徵函式就是正定函式。特徵函式比隨機變數的分布函式更易於處理。P.萊維正是用正定函式作工具對獨立隨機變數和的中心極限定理進行了比較統一完整的處理。正定函式在泛函分析中也經常遇到。事實上連續正定函式與某種連續正泛函一一對應。以R情況為例,R上連續正定函式?與M(R)(R上有界波萊爾測度所構成的對合巴拿赫代數)上連續正泛函
(4)
是一一對應的。此外，正定函式在調和分析中的地位也十分突出。交換群上的調和分析中的許多基本事實的建立都得力於正定函式這個概念。例如，傅立葉逆轉定理便敘述為式中∧表示傅立葉變換，∨表示傅立葉逆變換，弿表示G的對偶群。又如，普朗歇爾定理（它說，傅立葉變換是L2(G)到L2(弿)上的一個等距同構）的一個證明便利用了上述逆轉定理以及如下事實式中*表示卷積,B(G)是p(G)生成的複線性空間。至於在非交換群上的調和分析中，由於正定函式與連續酉表示的密切關係，以及它比連續酉表示更具體，它的作用也顯得越來越重要。此外，正定函式在複變函數、積分方程、微分方程的邊值問題、資訊理論等領域也都十分有用。
參考書目
E.Hewitt and K.A.Ross,αbstract harmonic Analysis,Vol.2, 2nd ed., Springer-Verlag, Berlin,1970.
J.Stewart, Positive Definite Functions and Generalizations, An Historical Survey,The Rocky Mountain Journal of Mathematics, Vol.6, pp.409～434, 1976.
