在控制理論中,通常需要判斷自治系統的穩定性。為了解決這一問題,我們有必要使用某些特殊的比較函式。K類函式如之的如下一類函式。
定義
K類函式
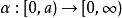 K類函式
K類函式定義(K類函式):一個連續函式 稱之為K類函式,如果
•該函式是嚴格遞增函式;
•該函式滿足
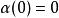 K類函式
K類函式K無窮類函式
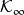 K類函式
K類函式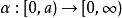 K類函式
K類函式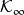 K類函式
K類函式定義( 類函式):一個連續函式 被稱為 屬於 類函式,如果
•該函式屬於K類函式;
•該函式滿足
•該函式滿足
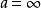 K類函式
K類函式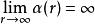 K類函式
K類函式套用
 K類函式
K類函式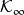 K類函式
K類函式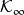 K類函式
K類函式一個非遞減正定函式 除了嚴格遞增外還滿足K類函式(或 類函式)的所有條件,那么該函式可以通過一下方式被K類函式(或 類函式)限制住上下界:
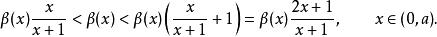 K類函式
K類函式因此,為了繼續相應的分析,這可以用連續不增正定函式,來限制我們感興趣函式的邊界。
例子
α(r) = tan^−1(r)是嚴格單調遞增的,因為α′(r) = 1/(1 + r2) > 0。所以該函式屬於K類函式,但該函式不是K∞類函式,因為limr→∞ α(r) = π/2 < ∞。
α(r) = r^c, 對於任意正實數c, 該函式是嚴格單調遞增的,因為α′(r) = cr^(c−1)> 0。此外,limr→∞ α(r) = ∞;因此,該函式屬於K∞類。
α(r) = min{r, r^2}是連續的嚴格增函式,且limr→∞ α(r) = ∞。因此,該函式屬於K∞類。
1.α(r) = tan^−1(r)是嚴格單調遞增的,因為α′(r) = 1/(1 + r2) > 0。所以該函式屬於K類函式,但該函式不是K∞類函式,因為limr→∞ α(r) = π/2 < ∞。
2.α(r) = r^c, 對於任意正實數c, 該函式是嚴格單調遞增的,因為α′(r) = cr^(c−1)> 0。此外,limr→∞ α(r) = ∞;因此,該函式屬於K∞類。
3.α(r) = min{r, r^2}是連續的嚴格增函式,且limr→∞ α(r) = ∞。因此,該函式屬於K∞類。
