簡介
正切半角公式，又稱萬能公式，這一組公式有四個功能：
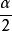正切半角公式將角統一為；
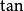正切半角公式將函式名稱統一為；
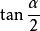正切半角公式任意實數都可以的形式表達，可用正切函式換元。
在某些積分中，可以將含有三角函式的積分變為有理分式的積分。
因此，這組公式被稱為以切表弦公式，簡稱以切表弦。它們是由二倍角公式求得的。
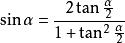正切半角公式
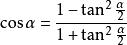正切半角公式
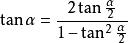正切半角公式 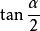正切半角公式而被稱為萬能公式的原因是利用的代換可以解決一些有關三角函式的積分 。
萬能公式的證明
由二倍角公式，有：
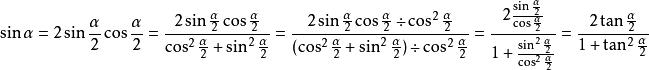正切半角公式再由同角三角函式間的關係，得出
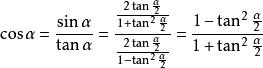正切半角公式幾何證明
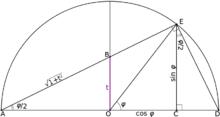正切半角公式
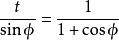正切半角公式
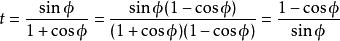正切半角公式在單位圓內，t = tan( φ/2)。根據相似關係，，可得出
。
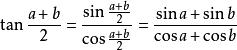正切半角公式顯然
。雙曲函式
此公式亦可以對雙曲函式起到類似的作用，由雙曲線右支上的一點(cosh θ,sinh θ)給出。從(−1,0)到 y軸給出了如下等式：
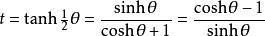正切半角公式可以得到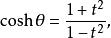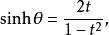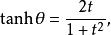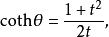
 正切半角公式 |  正切半角公式 |
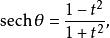 正切半角公式 |  正切半角公式 |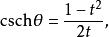
 正切半角公式 |  正切半角公式 |
和
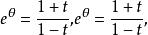正切半角公式卡爾·維爾斯特拉斯引入這個式子來省去查找原函式的麻煩。
θ在T而得出下面的雙曲反正切函式和自然對數之間的關係：
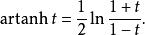正切半角公式