概述
定義正切函式是直角三角形中，某一銳角的對邊與鄰邊的比值。正切值的單位圓表示及正切函式圖像放在直角坐標系中（如圖）即tanθ=y/x三角函式三角函式是數學中屬於初等函式中的超越函式的一類函式。它們的本質是任意角的集合與一個比值的集合的變數之間的映射。通常的三角函式是在平面直角坐標系中定義的，其定義域為整個實數域。另一種定義是在直角三角形中，但並不完全。現代數學把它們描述成無窮數列的極限和微分方程的解，將其定義擴展到複數系。由於三角函式的周期性，它並不具有單值函式意義上的反函式。如下圖，正切是tanα=b/a餘切是cotα=a/b正弦是sinα=b/c餘弦是cosα=a/c正割是secα=c/a餘割是cscα=c/b正矢是versinθ=1-cosθ余矢是vercosθ=1-sinθ
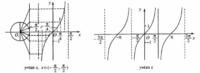正切值的單位圓表示及正切函式圖像正切函式
對於任意一個實數x，都對應著唯一的角（弧度制中等於這個實數），而這個角又對應著唯一確定的正切值tanx與它對應，按照這個對應法則建立的函式稱為正切函式。 形式是f(x)=tanx 正切函式是區別於正弦函式的又一三角函式，它與正弦函式的最大區別是定義域的不連續性。正切函式的性質
1、定義域：{x|x≠(π/2)+kπ,k∈Z} 2、值域：實數集R 3、奇偶性：奇函式 4、單調性：在區間(-π/2+kπ,π/2+kπ)，k∈Z上都是增函式 5、周期性：最小正周期π（可用π/|ω|來求） 6、最值：無最大值與最小值 7、零點：kπ,k∈Z 8、對稱性： 軸對稱：無對稱軸 中心對稱：關於點(kπ/2,0)對稱k∈Z 9、正切曲線的對稱中心：所有零點。坐標（kπ，0）（k∈Z）10、正切的兩角和與差公式：f(x+y)=f(x)+f(y)/1-f(x)f(y)f(x-y)=f(x)-f(y)/1+f(x)f(y)
正切值表
早期沒有電子計算器時，編制印行的角度-正切值查對表。現在已較少使用和印行。常用正切值：tan30°=√3/3，tan45°=1,tan60°=√3。tan90°不存在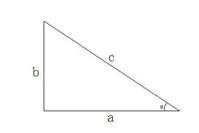
tanα=b/a