人物介紹
萊昂哈德·歐拉(Leonhard Euler ,1707年4月15日~1783年9月18日),瑞士數學家、自然科學家。1707年4月15日出生於瑞士的巴塞爾,1783年9月18日於俄國聖彼得堡去世。歐拉出生於牧師家庭,自幼受父親的影響。13歲時入讀巴塞爾大學,15歲大學畢業,16歲獲得碩士學位。歐拉是18世紀數學界最傑出的人物之一,他不但為數學界作出貢獻,更把整個數學推至物理的領域。他是數學史上最多產的數學家,平均每年寫出八百多頁的論文,還寫了大量的力學、分析學、幾何學、變分法等的課本,《無窮小分析引論》、《微分學原理》、《積分學原理》等都成為數學界中的經典著作。歐拉對數學的研究如此之廣泛,因此在許多數學的分支中也可經常見到以他的名字命名的重要常數、公式和定理。[1]此外歐拉還涉及建築學、彈道學、航海學等領域。瑞士教育與研究國務秘書Charles Kleiber曾表示:“沒有歐拉的眾多科學發現,今天的我們將過著完全不一樣的生活。”法國數學家拉普拉斯則認為:讀讀歐拉,他是所有人的老師。[2]2007年,為慶祝歐拉誕辰300周年,瑞士政府、中國科學院及中國教育部於2007年4月23日下午在北京的中國科學院文獻情報中心共同舉辦紀念活動,回顧歐拉的生平、工作以及對現代生活的影響。
拓撲學中
 歐拉數
歐拉數最通常的空間完整性,即空洞區域內空洞數量的度量,測量法稱為歐拉函式,它只用一個單一的數描述這些函式,稱為歐拉數。數量上,歐拉數=(空洞數)-(碎片數-1),這裡空洞數是外部多邊形自身包含的多邊形空洞數量,碎片數是碎片區域內多邊形的數量。有時歐拉數是不確定的。
線性代數中
線性代數中,歐拉數是對向量叢的一種刻畫。有向向量叢的零截面對於底空間的相交數。設ξ=(E,π,M)是n維有向向量叢,M是n維緊緻連通有向(無邊)微分流形。若將底空間M與ξ的零截面的像等同,則:
χ(ξ)=#(M,M)=#(M,M;E)
稱為向量叢ξ的歐拉數。設M如上述,ξ=TM,則χ(ξ)稱為流形M的歐拉特徵,記為χ(M)。例如,χ(S……2n)=2(因而S^2n上任何向量場均有零點),χ(S)=0.歐拉數是向量叢的同構不變數.在流形的切叢情形,得到在代數拓撲中有廣泛套用的拓撲不變數——流形的歐拉特徵數。
數學中
數學中,歐拉數是一組重要的常數,即函式sech t在t=0點的泰勒展開式:
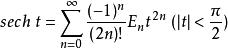 歐拉數
歐拉數的係數En。前幾個歐拉數為:
E0=1,E1=1,E2=5,E3=61,E4=1385,E5=50521,E6=2702765,……
歐拉數與歐拉多項式E(x)有關,
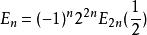 歐拉數
歐拉數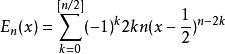 歐拉數
歐拉數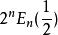 歐拉數
歐拉數有時也稱 為歐拉數。
流體力學中
流體力學中歐拉數的符號為Eu,描述動量傳遞的特徵數。
Eu=gΔP/ρu (若採用英制單位,g為轉換比率,單位為lb ft/lb hr ),
Eu=ΔP/ρu (若採用標準單位,不需加轉換比率)
其中Eu定義為歐拉數。△p為壓力差;ρ為物體的體積質量;υ為特徵速度。SI單位:1(一)。與通常量的符號的表達不同的是,特徵數的符號均由兩個字母組成。當特徵數符號在乘積中作為相乘的因數時,建議其符號與其他符號之間空一個間隔,或用乘號或括弧隔開。
它反映了流場壓力降與其動壓頭之間的相對關係,體現了在流動過程中動量損失率的相對大小。

