基本介紹
歐拉-麥克勞林公式 設函式f(x)在區間[a,b]上有直到v階連續微商，當v≥2時，給出歐拉-麥克勞林公式：
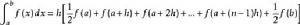歐拉一麥克勞林公式
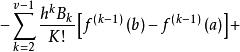歐拉一麥克勞林公式
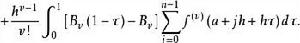歐拉一麥克勞林公式
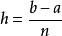歐拉一麥克勞林公式這裡 ，B是伯努利數，B(x)是伯努利多項式。可利用伯努利(Bernoulli)多項式的性質證明歐拉-麥克勞林公式。
相關說明
下面對歐拉-麥克勞林公式作些說明：
1．係數中用到的 伯努利數和 伯努利多項式都可由表查得，故此公式用起來很方便。
2．歐拉-麥克勞林公式可以被看作[a，b]上改善了的梯形公式，右端第二部分可看成修正項，最後那項看成餘項。
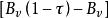歐拉一麥克勞林公式
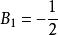歐拉一麥克勞林公式3．歐拉-麥克勞林公式被套用時一般都取v為偶數，這是因為估計餘項時使得餘項里積分號下的因子 不變號的緣故。又因具奇標號的伯努利數等於零(除 外)。所以歐拉-麥克勞林公式可以寫成
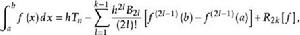歐拉一麥克勞林公式其中
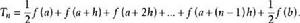歐拉一麥克勞林公式
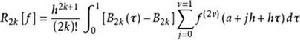歐拉一麥克勞林公式
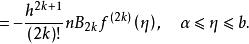歐拉一麥克勞林公式
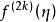歐拉一麥克勞林公式4．由於上面的餘項表達式中包含有伯努利數，而伯努利數是隨著k之增大而增大非常快的。故餘項有時會趨向無窮。故使用這個公式時不應把k取得太大。一般用起來取2k=6，這時相應的伯努利數取最小值。又因餘項里含有因子 也是使k不宜取得過大的原因。
