基本介紹
機率分布函式
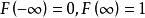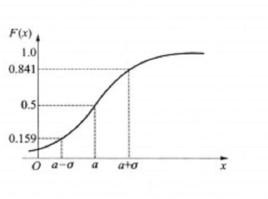
機率分布函式機率分布函式是描述隨機變數取值分布規律的數學表示。對於任何實數x，事件[X<x]的機率當然是一個x的函式。令 ，顯然有 ，稱F(x)為隨機變數X的分布函式。所以，分布函式F(x)完全決定了事件[a≤X≤b]的機率，或者說分布函式F(x)完整地描述了隨機變數X的統計特性。
常見的離散型隨機變數分布模型有“0-1分布”、二項式分布、泊松分布等；連續型隨機變數分布模型有均勻分布、常態分配、瑞利分布等。
分類
離散型隨機變數的機率分布
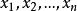機率分布函式
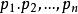機率分布函式對於離散型隨機變數，設 為變數X的取值，而 為對應上述取值的機率，則離散型隨機變數X的機率分布為
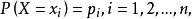機率分布函式
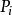機率分布函式
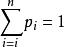機率分布函式且機率 應滿足條 。因此，離散型隨機變數X的機率分布函式為
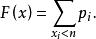機率分布函式連續型隨機變數的機率分布
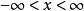機率分布函式
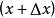機率分布函式對於連續型隨機變數，設變數X取值於區間(a，b)，並假設其分布函式F(x)為單調增函式，且在 間可微分及其導數F’(x)在此區間連續，則變數X落在x至 區間內的機率為
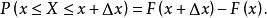機率分布函式
機率分布函式為描述其機率分布規律，這時不可能用分布列表示，而是引入“機率分布密度函式”的新概念。定義機率分布函式F(x)的導數F’(x)為機率分布密度函式f(x)，即
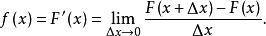機率分布函式於是連續型隨機變數X的機率分布函式可寫為常用的機率積分公式的形式：
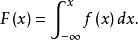機率分布函式
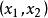機率分布函式這樣，只要已知某一連續型隨機變數X的機率分布密度函式f(x)，即可求得X落在某一區間 內的機率：
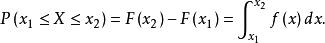機率分布函式與離散型隨機變數的機率函式一樣．對於分布密度函式，有
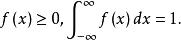機率分布函式 機率分布函式連續型隨機變數的分布密度函式 ．以及與它對應的分布函式F(x)的圖形分別如圖1和圖2所示。有時稱f(x)的圖形為分布曲線，而稱F(x)的圖形為累積分布曲線。
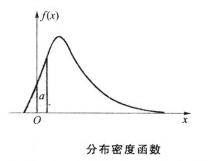圖1
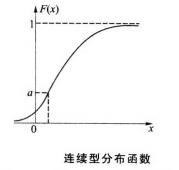圖2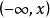
機率分布函式分布函式F(x)是一個普通函式。正是通過它才能用數學分析的方法來研究隨機變數。如果將X看成是數軸上隨機點的坐標，那么分布函式F(x)在x處的函式值就表示X落在區間 的機率。
分布函式F(x)具有下述基本性質：
①F(x)為單凋非降函式：
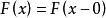機率分布函式② 左連續；
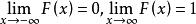機率分布函式③ 。
綜上所述，機率分布函式是隨機變數特性的表征，它決定了隨機變數取值的分布規律，只要已知了機率分布函式，就可以算出隨機變數落於某處的機率。
